664A - Complicated GCD

Author of the idea — GlebsHP

We examine two cases:

1. a = b — the segment consists of a single number, hence the answer is a.
2. a < b — we have gcd(a, a + 1, a + 2, ..., b) = gcd(gcd(a, a + 1), a + 2, ..., b) = gcd(1, a + 2, ..., b) = 1.

#include <bits/stdc++.h>

using namespace std;

int main() {
    string a, b;
    cin >> a >> b;

    if (a == b) cout << a;
    else cout << 1;

    return 0;
}

663A - Rebus

Author of the idea — gen

First we check whether any solution exists at all. For that purpose, we calculate the number of positive (the first one and any other with the  +  sign) and negative elements (with the  -  sign) in the sum. Let them be pos and neg, respectively. Then the minimum value of the sum that can be possibly obtained is equal to min = (1 · pos - n · neg), as each positive number can be 1, but all negative can be  - n. Similarly, the maximum possible value is equal to max = (n · pos - 1 · neg). The solution therefore exists if and only if min ≤ n ≤ max.

Now suppose a solution exists. Let's insert the numbers into the sum one by one from left to right. Suppose that we have determined the numbers for some prefix of the expression with the sum of S. Let the sign of the current unknown be sgn ( + 1 or  - 1) and there are some unknown numbers left to the right, excluding the examined unknown, among them pos_left positive and neg_left negative elements. Suppose that the current unknown number takes value x. How do we find out whether this leads to a solution? The answer is: in the same way we checked it in the beginning of the solution. Examine the smallest and the largest values of the total sum that we can get. These are equal to min_left = (S + sgn · x + pos_left - n · neg_left) and max_left = (S + sgn · x + n · pos_left - neg_left), respectively. Then we may set the current number to x, if min_left ≤ n ≤ max_left holds. To find the value of x, we can solve a system of inequalities, but it is easier simply to check all possible values from 1 to n.

BONUS Let k be the number of unknowns in the rebus. Prove that the complexity of the described solution (implementation shown below) is O(k² + n), not O(k · n).

#include<bits/stdc++.h>

using namespace std;

char s[100];

int main() {
    int k = 0, n, pos = 1, neg = 0;
    while (true) {
        char c;
        scanf(" %c", &c);
        scanf(" %c", &c);

        if (c == '=') break;
        if (c == '+') pos++;
        if (c == '-') neg++;

        s[k++] = c;
    }

    scanf("%d", &n);

    if (pos - n * neg > n || n * pos - neg < n) {
        printf("Impossible\\n");

        return 0;
    }

    printf("Possible\\n");

    int S = 0;
    for (int i = 0; i < k; i++) {
        int sgn = 1;
        if (i > 0 && s[i - 1] == '-') sgn = -1;

        if (sgn == 1) pos--;
        if (sgn == -1) neg--;

        for (int x = 1; x <= n; x++)
            if (S + x * sgn + pos - n * neg <= n && S + x * sgn + n * pos - neg >= n) {
                printf("%d %c ", x, s[i]);

                S += x * sgn;

                break;
            }
	}

    printf("%d = %d\\n", abs(n - m), n);

    return 0;
}

662D - International Olympiad

Author of the idea — Alex_2oo8

Consider the abbreviations that are given to the first Olympiads. The first 10 Olympiads (from year 1989 to year 1998) receive one-digit abbreviations (IAO'9, IAO'0, ..., IAO'8). The next 100 Olympiads (1999 - 2098) obtain two-digit abbreviations, because all one-digit abbreviations are already taken, but the last two digits of 100 consecutive integers are pairwise different. Similarly, the next 1000 Olympiads get three-digit abbreviations and so on.

Now examine the inversed problem (extract the year from an abbreviation). Let the abbreviation have k digits, then we know that all Olympiads with abbreviations of lengths (k - 1), (k - 2), ..., 1 have passed before this one. The number of such Olympiads is 10^k - 1 + 10^k - 2 + ... + 10¹ = F and the current Olympiad was one of the 10^k of the following. Therefore this Olympiad was held in years between (1989 + F) and (1989 + F + 10^k - 1). As this segment consists of exactly 10^k consecutive natural numbers, it contains a single number with a k-digit suffix that matches the current abbreviation. It is also the corresponding year.

#include <bits/stdc++.h>

using namespace std;

char s[42];

int main() {
    int n;
    scanf("%d", &n);
    while (n--) {
        scanf(" %s", s);
        
        int k = strlen(s + 4), year = atoi(s + 4), F = 0, tenPow = 10;
        for (int i = 1; i < k; i++) {
            F += tenPow;
            tenPow *= 10;
        }
        
        while (year < 1989 + F) year += tenPow;
        
        printf("%d\\n", year);
    }

    return 0;
}

662B - Graph Coloring

Author of the problem — gen

Examine the two choices for the final color separately, and pick the best option afterwards. Now suppose we want to color the edges red.

Each vertex should be recolored at most once, since choosing a vertex two times changes nothing (even if the moves are not consecutive). Thus we need to split the vertices into two sets S and T, the vertices that are recolored and the vertices that are not affected, respectively. Let u and v be two vertices connected by a red edge. Then for the color to remain red, both u and v should belong to the same set (either S or T). On the other hand, if u and v are connected by a blue edge, then exactly one of the vertices should be recolored. In that case u and v should belong to different sets (one to S and the other to T).

This problem reduces to 0-1 graph coloring, which can be solved by either DFS or BFS. As the graph may be disconnected, we need to process the components separately. If any component does not have a 0-1 coloring, there is no solution. Otherwise we need to add the smallest of the two partite sets of the 0-1 coloring of this component to S, as we require S to be of minimum size.

#include<bits/stdc++.h>

using namespace std;

const int MX = 100000;

int n, vis[MX];
vector<pair<int, char>> G[MX];
vector<int> part[3];

bool dfs(int v, int p, char c) {
    if (vis[v] != 0) {
        return vis[v] == p;
    }

    vis[v] = p;
    part[p].push_back(v);

    for (auto x : G[v]) {
        if (dfs(x.first, x.second == c ? p : p ^ 3, c) == false)
            return false;
    }

    return true;
}

vector<int> solve(char c) {
    memset(vis, 0, sizeof vis);

    vector<int> ans;
    for (int i = 0; i < n; i++)
        if (vis[i] == 0) {
            part[1].clear();
            part[2].clear();

            if (dfs(i, 1, c) == false) {
                for (int j = 0; j < n + 1; j++) ans.push_back(-1);

                return ans;
            }

            int f = 1;
            if (part[2].size() < part[1].size()) f = 2;

            ans.insert(ans.end(), part[f].begin(), part[f].end());
        }

    return ans;
}

int main() {
    int m;
    scanf("%d %d", &n, &m);
    for (int i = 0; i < m; i++) {
        int u, v;
        char c;
        scanf("%d %d %c", &u, &v, &c);
        u--;
        v--;

        G[u].emplace_back(v, c);
        G[v].emplace_back(u, c);
    }

    auto f = solve('R');
    auto g = solve('B');

    if (g.size() < f.size()) f = g;

    if (f.size() > n) {
        printf("-1\\n");

        return 0;
    }

    printf("%d\\n", (int)f.size());
    for (int x : f) printf("%d ", x + 1);
    printf("\\n");

    return 0;
}

662A - Gambling Nim

Author of the idea — GlebsHP

It is known that the first player loses if and only if the xor-sum of all numbers is 0. Therefore the problem essentially asks to calculate the number of ways to arrange the cards in such a fashion that the xor-sum of the numbers on the upper sides of the cards is equal to zero.

Let 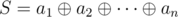and 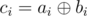. Suppose that the cards with indices j₁, j₂, ..., j_k are faced with numbers of type b and all the others with numbers of type a. Then the xor-sum of this arrangement is equal to 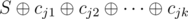, that is, 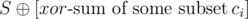. Hence we want to find the number of subsets c_i with xor-sum of S.

Note that we can replace c₁ with , as applying c₁ is the same as applying 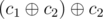. Thus we can freely replace {c₁, c₂} with and c₂ with 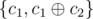. This means that we can apply the following procedure to simplify the set of c_i:

1. Pick c_f with the most significant bit set to one
2. Replace each c_i with the bit in that position set to one to
3. Remove c_f from the set
4. Repeat steps 1-5 with the remaining set
5. Add c_f back to the set

After this procedure we get a set that contains k zeros and n - k numbers with the property that the positions of the most significant bit set to one strictly decrease. How do we check now whether it is possible to obtain a subset with xor-sum S? As we have at most one number with a one in the most significant bit, then it tells us whether we should include that number in the subset or not. Similarly we apply the same argument for all other bits. If we don't obtain a subset with the xor-sum equal to S, then there is no such subset at all. If we do get a subset with xor-sum S, then the total number of such subsets is equal to 2^k, as for each of the n - k non-zero numbers we already know whether it must be include in such a subset or not, but any subset of k zeros doesn't change the xor-sum. In this case the probability of the second player winning the game is equal to 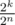, so the first player wins with probability .

#include <bits/stdc++.h>

using namespace std;

const int size = 1000 * 1000 + 1;
const int ssize = 100;

int n;
long long a[size], b[size];
long long ort[ssize];
long long p[ssize];

int main() {
    long long cur = 0ll;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%lld%lld", &a[i], &b[i]);
        cur ^= a[i];
        a[i] ^= b[i];
    }
    a[n] = cur;

    int len = 0;
    for (int i = 0; i <= n; i++) {
        for (int j = 0; j < len; j++) {
            if (a[i] & p[j])
                a[i] ^= ort[j];
        }
        if (a[i]) {
            ort[len++] = a[i];
            p[len - 1] = ((a[i] ^ (a[i] - 1)) + 1) >> 1;
        }        
    }
    if (a[n]) {
        printf("1/1\\n");
    } else {
        printf("%lld/%lld\\n", (1ll << len) - 1, (1ll << len));
    }

    return 0;
}

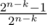662C - Binary Table

Author of the idea — Alex_2oo8

First let's examine a slow solution that works in O(2ⁿ · m). Since each row can be either inverted or not, the set of options of how we can invert the rows may be encoded in a bitmask of length n, an integer from 0 to (2ⁿ - 1), where the i-th bit is equal to 1 if and only if we invert the i-th row. Each column also represents a bitmask of length n (the bits correspond to the values of that row in each of the n rows). Let the bitmask of the i-th column be col_i, and the bitmask of the inverted rows be mask. After inverting the rows the i-th column will become 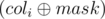. Suppose that 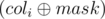contains 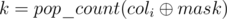ones. Then we can obtain either k or (n - k) ones in this column, depending on whether we invert the i-th column itself. It follows that for a fixed bitmask mask the minimum possible number of ones that can be obtained is equal to .

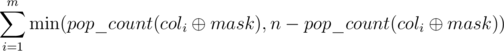Now we want to calculate this sum faster than O(m). Note that we are not interested in the value of the mask 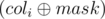itself, but only in the number of ones it contains (from 0 to n). Therefore we may group the columns by the value of 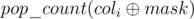. Let dp[k][mask] be the number of such i that 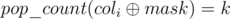, then for a fixed bitmask mask we can calculate the sum in O(n) — .

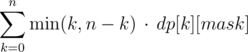What remains is to calculate the value of dp[k][mask] in a quick way. As the name suggests, we can use dynamic programming for this purpose. The value of dp[0][mask] can be found in O(m) for all bitmasks mask: each column col_i increases dp[0][col_i] by 1. For k > 0, col_i and mask differ in exactly k bits. Suppose mask and col_i differ in position p. Then col_i and 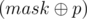differ in exactly (k - 1) bits. The number of such columns is equal to 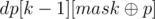, except we counted in also the number of columns col_i that differ with 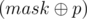in bit p (thus, mask and col_i have the same value in bit p). Thus we need to subtract dp[k - 2][mask], but again, except the columns among these that differ with mask in bit p. Let 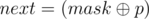; by expanding this inclusion-exclusion type argument, we get that the number of masks we are interested in can be expressed as dp[k - 1][next] - dp[k - 2][mask] + dp[k - 3][next] - dp[k - 4][mask] + dp[k - 5][next] - .... By summing all these expressions for each bit p from 0 to n, we get dp[k][mask] · k, since each column is counted in k times (for each of the bits p where the column differs from mask).

Therefore, we are now able to count the values of dp[k][mask] in time O(2ⁿ · n³) using the following recurrence:

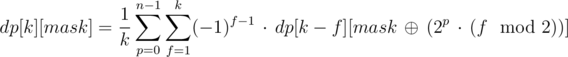
This is still a tad slow, but we can speed it up to O(2ⁿ · n²), for example, in a following fashion:

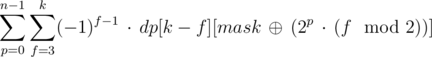
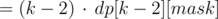
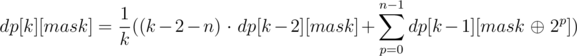
BONUS Are you able to come up with an even faster solution?

#include<bits/stdc++.h>

using namespace std;

char s[100000];
int col[100000], dp[21][1 << 20];

int main() {
    int n, m;
    scanf("%d %d", &n, &m);
    for (int i = 0; i < n; i++) {
        scanf(" %s", s);

        for (int j = 0; j < m; j++) col[j] |= (s[j] - '0') << i;
    }

    for (int i = 0; i < m; i++) dp[0][col[i]]++;

    for (int k = 1; k <= n; k++)
        for (int mask = 0; mask < (1 << n); mask++) {
            int sum = k > 1 ? (k - 2 - n) * dp[k - 2][mask] : 0;
            for (int p = 0; p < n; p++) sum += dp[k - 1][mask ^ (1 << p)];

            dp[k][mask] = sum / k;
        }

    int ans = n * m;
    for (int mask = 0; mask < (1 << n); mask++) {
        int cnt = 0;
        for (int k = 0; k <= n; k++) cnt += min(k, n - k) * dp[k][mask];

        ans = min(ans, cnt);
    }

    printf("%d\\n", ans);

    return 0;
}

662E - To Hack or not to Hack

Author of the idea — Alex_2oo8

Observation number one — as you are the only participant who is able to hack, the total score of any other participant cannot exceed 9000 (3 problems for 3000 points). Hence hacking at least 90 solutions automatically guarantees the first place (the hacks alone increase the score by 9000 points).

Now we are left with the problem where the number of hacks we make is at most 90. We can try each of the 6³ possible score assignments for the problems in the end of the round. As we know the final score for each problem, we can calculate the maximum number of hacks we are allowed to make so the problem gets the assigned score. This is also the exact amount of hacks we will make in that problem. As we know the number of hacks we will make, we can calculate our final total score. Now there are at most 90 participants who we can possibly hack. We are interested only in those who are on top of us. By hacking we want to make their final score less than that of us. This problem can by solved by means of dynamic programming:

dp[p][i][j][k] — the maximum number of participants among the top p, whom we can push below us by hacking first problem i times, second problem j times and third problem k times.

The recurrence: we pick a subset of solutions of the current participant that we will hack, and if after these hacks we will push him below us, we update the corresponding dp state. For example, if it is enough to hack the first and the third problems, then dp[p + 1][i + 1][j][k + 1] = max(dp[p + 1][i + 1][j][k + 1], dp[p][i][j][k] + 1)

BONUS Can you solve this problem if each hack gives only 10 points, not 100?

#include<bits/stdc++.h>

#define time ololo

using namespace std;

int time[5000][3], n, solved[3], canHack[3], score[3], willHack[3], bestPlace, dp[2][90][90][90], ci, li;

int submissionScore(int sc, int tm) {
    if (tm == 0) return 0;

    return sc * (250 - abs(tm)) / 250;
}

int calcScore(int p) {
    int sum = 0;
    for (int i = 0; i < 3; i++) sum += submissionScore(score[i], time[p][i]);

    return sum;
}

int countHacks(int p) {
    int cnt = 0;
    for (int i = 0; i < 3; i++) cnt += time[p][i] < 0;

    return cnt;
}

int solve() {
    memset(dp, 0, sizeof dp);

    int myScore = 0;
    for (int i = 0; i < 3; i++) myScore += 100 * willHack[i] + submissionScore(score[i], time[0][i]);

    ci = 0;
    li = 1;
    for (int p = 1; p < n; p++)
        if (countHacks(p) > 0 && calcScore(p) > myScore) {
            ci ^= 1;
            li ^= 1;

            for (int i = 0; i <= willHack[0]; i++)
                for (int j = 0; j <= willHack[1]; j++)
                    for (int k = 0; k <= willHack[2]; k++)
                        dp[ci][i][j][k] = dp[li][i][j][k];

            for (int ii = 0; ii < 2; ii++)
                for (int jj = 0; jj < 2; jj++)
                    for (int kk = 0; kk < 2; kk++) {
                        if (ii == 1 && time[p][0] >= 0) continue;
                        if (jj == 1 && time[p][1] >= 0) continue;
                        if (kk == 1 && time[p][2] >= 0) continue;

                        int s = submissionScore(score[0], time[p][0]) * (ii ^ 1)
                              + submissionScore(score[1], time[p][1]) * (jj ^ 1)
                              + submissionScore(score[2], time[p][2]) * (kk ^ 1);

                        if (s > myScore) continue;

                        for (int i = ii; i <= willHack[0]; i++)
                            for (int j = jj; j <= willHack[1]; j++)
                                for (int k = kk; k <= willHack[2]; k++)
                                    dp[ci][i][j][k] = max(dp[ci][i][j][k], dp[li][i - ii][j - jj][k - kk] + 1);
                    }
        }

    int res = 1 - dp[ci][willHack[0]][willHack[1]][willHack[2]];
    for (int p = 1; p < n; p++) if (calcScore(p) > myScore) res++;

    return res;
}

void brute(int p) {
    if (p == 3) {
        int res = solve();

        bestPlace = min(bestPlace, res);

        return;
    }

    for (int i = 0; i < 6; i++) {
        int mn = i == 5 ? 0 : (n >> (i + 1)) + 1;
        int mx = (n >> i);

        if (solved[p] >= mn && solved[p] - canHack[p] <= mx) {
            score[p] = 500 * (i + 1);
            willHack[p] = min(canHack[p], solved[p] - mn);

            brute(p + 1);
        }
    }
}

int main() {
    memset(solved, 0, sizeof solved);
    memset(canHack, 0, sizeof canHack);
    
    scanf("%d", &n);
    for (int i = 0; i < n; i++)
        for (int j = 0; j < 3; j++) {
            scanf("%d", &time[i][j]);

            solved[j] += time[i][j] != 0;
            canHack[j] += time[i][j] < 0;
        }

    if (canHack[0] + canHack[1] + canHack[2] > 89) {
        printf("1\\n");

        return 0;
    }

    bestPlace = n;
    brute(0);

    printf("%d\\n", bestPlace);

    return 0;
}