Hello CodeForces Community!
I am glad to share that HackerRank's World Codesprint April is scheduled on 29-April-2016 at 16:00 UTC. Contest duration is 24 hours.
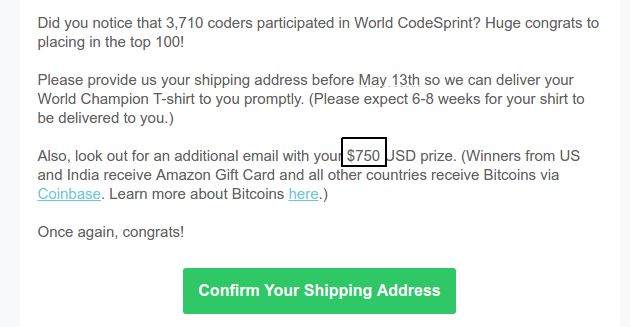
Go ahead and register now to show off your coding abilities, and win upto $2000 Amazon gift cards/bitcoins and tshirts. [Note: Winners from US and India will receive Amazon Gift Cards. Winners from other countries will receive equivalent USD amount in bitcoins.]
The problems were prepared by malcolm, Radewoosh, svanidz1, ma5termind and Shafaet. Thanks to wanbo for testing the problems and forthright48 for helping with editorials.
The contest will be rated. If two person gets same score, the person who reached the score first will be ranked higher.
Editorials will be live soon after the contest ends, I invite everyone from experts to beginners to participate and solve challenges. I hope everyone will enjoy the contest.
Edit: The contest is less than 15 minutes away.
Score distribution: 15-20-40-60-60-80-80-100
Update:
The contest is over! Congratulation to the winners:
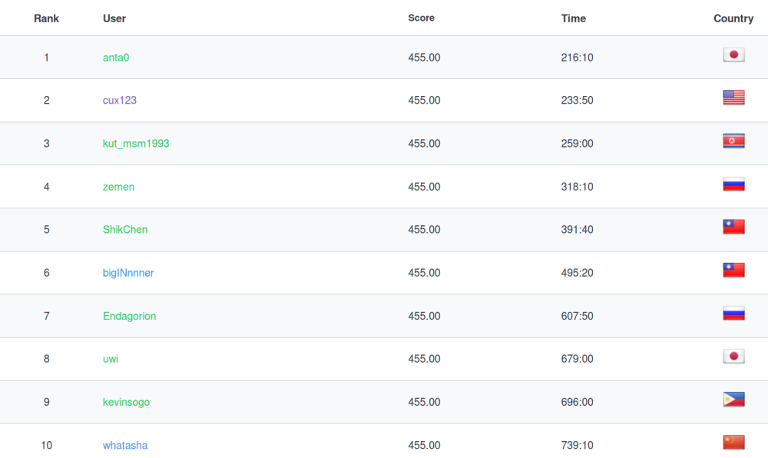
Ratings will be updated soon. Let us know if you like this round and don't forget to join the next contest HourRank-8!
Update:
Details editorial for Move the Coins problem is posted here.











win upto $2000 Amazon gift cards/bitcoins, medals and tshirts.I can't find medals amongst the prizes.
Oops the Medals was for last world codesprint, not this one, edited the post. Thanks.
Unfortunate intersection with Codeforces Round.
This was scheduled since like forever, CF round was only announced a short while before the contest.
Yep, I know) Just a statement of fact.
I enjoyed the problems. Much better than the last CF round.
Really glad to hear that. There will be another world code-sprint in May, hoping to see you there!
I have not seen problems from the latest CF but I don't regret that I missed that round because of Codesprint. Very cool problems, especially one about coins on the tree.
I am very happy to know a top guy like you liked my game problem :D. Thanks.
problem 7 was really great. I enjoyed it a lot! Thanks for all your effort (and nice prizes — which will make a great dinner with my family)
Missed CF round because of the Codesprint — and people say I've done nothing wrong.
Unfortunately I have no much time to participate, but I liked the tasks I was able to solve. Tasks about greedy KMP and nim on the tree (4th and 5th) were already enjoying, so I wonder how cool might be the next ones?
Can someone explain like I'm five a solution to the "Sum of the Maximums" problem? I don't understand how to boost the solution in editorial.
solution to the "Sum of the Maximums" problem? I don't understand how to boost the solution in editorial.
I solved it using MO's techinque in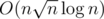 (after some fight it passed).
(after some fight it passed).
Hey.Can you share your approach?I was trying this with MO's algorithm but couldn't figure out a way to add/remove a new number to the existing subarray in sublinear time.
Thanks.
I also did it using MO's but only when we can add an element to the range and not subtract. It passed well in time. My approach was as follows :
For every block , sort the queries by increasing R (as in MO's). Now for every query [L,R] , calculate the answers independently for [L,mid] and [mid,R] where mid is the end point of that block. For every query we can spend O(root(N)) for [L,mid] and since R is always increasing the overall time for all [mid,R] queries of this square root block would be O(N). Now the only step left is the merging step i.e. getting the answer of [L,R] from [L,mid] and [mid,R]. To do this, while processing the [mid,R] interval maintain an array containing only elements in increasing order (that occur along the path). Then, iterate over all elements from [L,mid] and to get the contribution of i'th element (i.e. sum of max of all subarrays starting at this point) we binary search to get the first position j in the increasing array maintained such that A[arr[j]] >= (max of all A[k], k goes from i to mid) and then add the contribution accordingly (see code for more implementation details.)
You can have a look at my code here : http://pastebin.com/DhDgmY4V
We use standard MO — aproach. So we sort queries, start with first query and then change one query to another. There are four types of moves:
add-left
add-right
subtract-left
subtract-right
Let us first focus on add_left: We have the answer for the interval [L, R] and we want to compute the answer for the interval [L - 1, R]. So we just want to know
How to compute that? I use "ladder" technique. We have two tables: $next_right[N][log_N]$ and result_right[N][log_N], which means:
next_right[i][h] is 2h-th element to the right on the longest increasing sequence starting at A[i].
result_right[i][h] is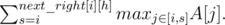
Those tables can be easly computed for example next_right[i][h] = next_right[next_right[i][h - 1]][h - 1] and result_right[i][h] = result_right[i][h - 1] + result_right[next_right[i][h - 1]][h - 1] and so on.
In order to compute F(L - 1, R) we use that ladders. We start at L - 1 and want to reach R. We process ladders from log_N to 0, if the ladder goes before R then we use it, otherwise we skip it.
In the same manner we deal with add-right, subtract-left, subtract-right.
I also used Mo's algorithm but did all add and subtract operation in
O(1)with some precalculation. It's useful to see that when going from [L-1,R] to [L,R],and we want to add sum of maximums of segments [L,x] , L<=x<=R.You go to first element bigger than A[L] (let's say it has position x),add to solution(x-L)*A[L],then next bigger than A[x] .... and so on.(until next bigger >R,when you add (R-x+1)*A[x]). Arraynextbig[i]=first bigger element from right of i,and can be computed inO(n).Ok,this approach is slow,it can take
O(R-L+1)steps. We can do better. Make a tree with edges(nextbig[i],i),precalculate partial sums on tree (root being position n+1),likeval[i]=(nextbig[i]-i)*A[i]andsum[i]=sum[nextbig[i]]+val[i]. Now moving to nextbig[i] is just going up on tree. It would be nice if we can find the last node we reach until we go after limit R.And this is actually the maximum element on segment [L,R] with minimum position of all positions in segment. Now this can be answered with RMQ table precalculated in
O(n*log). Take care that val[max_seg] can include segments with are not in [L,R]. So let's say minimum position of maximum is x. The answer issum[L]-sum[x]+(R-x+1)*A[x].(for every node from path L to x excluding x is safe to add all segments where that node is maximum,which is equivalent to val[i])For O(NlgN) solution, imagine a N * N grid filled with RMQ[i, j]. In such grid, there is N rectangle (which is derived from every element) filling whole grid.
To enumerate these rectangles, you can use this divide & conquer algorithm. This algorithm calculates the area where the given elements affect the grid, and it's clear that this algorithm fills the whole grid.
Now it became a geometry problem. For every queries (which is also a rectangle) , you should calculate the sum of (intersection area) * (value of rectangle).
This problem can be solved offline using segment tree + plane sweeping. split every rectangle [sx, ex, sy, ey, v] to [1, sx-1, sy, ey, -v] + [1, ex, sy, ey, v] and sweep from x coordinate. Now answer each query by
code : http://ideone.com/rLzNjF
Could you describe reduction to geometrical problem in more details again?
Problem 8 : this problem can be solved without HLD.
For every vertex v. maintain ans[i] = sum of value from path [root — i]. If we maintained it correctly, we can answer the query by returning ans[s] + ans[e] — ans[lca(s,e)] — ans[parent(lca(s, e))].
For speedup, we use the identity Sum(F(i)) = F(i+2) — 1. Now addition query "U v k" can be transformed into "add F(k + depth[x] — depth[v] + 2) — F(k + 1) for all x lying in subtree of v"
Adding -F(k+1) to subtree can be done with matrix + binary power + dfs numbering + fenwick tree.
To add F(t + depth[x]) to subtree, we can do the same with above — just store matrix in fenwick tree. We add F^(t) (F = {{1, 1}, {1, 0}} to range, and calculate F^(depth) * BIT.Query(v) matrix in query stage. Now the problem is solved in O((N + Q)lgN).
Note that the t in F^(t) might be negative, but it can be solved by powering inversion matrix of F.
code : http://ideone.com/MigTNx (sorry for messy codes)
Can anyone suggest me some other problems like "Lovely triplets" (prob 6) ? I really like this problem.
Maybe you want to look at problems with tag "constructive algorithms" on CodeForces.
Would anyone care to explain why, in Move the Coins, the nimber is the xor of all odd-level nodes' values? Maybe proving this once you have the hypothesis is not so difficult, so, more importantly, how did you come to that idea?
Do you think about this tutorial ?
Didn't see that, thanks. I'll take a look.
http://lightoj.com/volume_showproblem.php?problem=1393 You can also try another problem in similar idea.
I really like the problem set! All problems are nice, most especially the middle ones:
For Fibonacci Numbers Tree, I used Binet's formula to convert Fibonacci numbers to powers of φ. Then I just worked on the field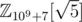 in all my calculations. Using powers of φ allows for simple identities like φa + b = φaφb in replacement of Fa + b = Fa - 1·Fb + Fa·Fb + 1. It's not necessarily more efficient, but that's okay.
in all my calculations. Using powers of φ allows for simple identities like φa + b = φaφb in replacement of Fa + b = Fa - 1·Fb + Fa·Fb + 1. It's not necessarily more efficient, but that's okay.
Where can I specify my BTC wallet number to receive the money? Or the organizers will contact me by email?
In the order of difficulty order: easy, easy, a bit harder, good, good, good, boring, boring.
In particular, I knew how to solve the sum of maximums because I contemplated it in a problem I set here on CF (you can find it easily). At that time, I thought it's too much work with nothing creative (just non-trivial Fenwick trees) and decided to let O(NQ) solutions pass.
The last problem was easily solvable with sqrt decomposition: after each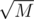 update queries, recalculate the sums on all paths from the root; when computing an answer to a query, take the last sum obtained that way and add everything from update queries (a prefix sum of Fibonacci numbers is a Fib. number again, big indices can be dealt with by matrix multiplication). Problems 4-6 were far more interesting to me than this.
update queries, recalculate the sums on all paths from the root; when computing an answer to a query, take the last sum obtained that way and add everything from update queries (a prefix sum of Fibonacci numbers is a Fib. number again, big indices can be dealt with by matrix multiplication). Problems 4-6 were far more interesting to me than this.
There must be something wrong <(") Though I like it more this way :P