Спасибо всем участникам нашего соревнования за множество успешных посылок по задачам!
Этот комплект для вас подготовили: Romka, Chmel_Tolstiy и Ixanezis. Спасибо Ивану Gassa Казменко за помощь в подготовке текстов задач и разбора.
Задача А. Правописание
В задаче достаточно маленькие ограничения для того, чтобы можно было решить её "в лоб", за O(N2L), где N — количество слов в словаре, а L — длина слова.
Для получения такой сложности достаточно для каждого слова проверить, может ли оно являться тем самым "правильным" словом, не содержащим ошибок. Для этого нужно проверить, что все остальные слова отличаются от него не более чем в одной букве: проходим по всем словам ещё раз и вычисляем количество позиций, в которых выбранное слово отличается от всех других слов. Если для всех слов отличия есть не более чем в одной позиции, выбранное слово вполне имеет право быть тем "правильным" словом, что мы ищем.
Для этой задачи также существует более быстрое решение за O(NL), но его не обязательно было здесь применять.
Задача B. Голосовые предупреждения
Для каждого варианта предупреждения вычислим расстояние Di, за которое нужно начинать произносить данный вариант. Это можно сделать по формуле: Di = Xi + V·(ti + Tphrase). После вычисления нужно выбрать минимальный вариант, а среди нескольких одинаковых — вариант с минимальным индексом, как требуется в условии задачи.
Задача C. Турнир по настольному теннису
Для решения этой задачи необходимо сделать следующее наблюдение. Из условия задачи следует, что участники соревнования набрали 2·N - 2, 2·N - 3, \ldots, N - 1 очков. А отсюда следует, что победитель выиграл матчи у всех остальных, участник, занявший второе место, победил всех, кроме победителя, и так далее. Участник, занявший последнее место, проиграл все матчи.
Следовательно, если мы зафиксируем порядок номеров участников, в котором они должны закончить турнир, то мы можем найти вероятность именно такого окончательного исхода. Для этого достаточно найти произведение необходимых вероятностей из матрицы вероятностей pij. Для генерации всех перестановок можно использовать метод std::next_permutation (C++) или, к примеру, реализовать рекурсивный перебор.
Таким образом, исходная задача решается описанным алгоритмом за время O(N2·N!). Используя идеи динамического программирования, этот подход можно ускорить и получить алгоритм, работающий за O(N·2N).
Задача D. Числовое сжатие
Будем решать задачу методом динамического программирования. К задаче есть несколько различных подходов, мы опишем только один из них.
Заметим, что битовых последовательностей длины L c K чередующимися группами битов, начинающихся с группы с нулевым битом, в точности C(L - 1, K - 1). Действительно, так как все группы не пустые, то нам среди L - 1 границ между соседними элементами последовательности битов нужно выбрать K - 1, которые и будут разделять соседние группы с различными битами.
Рассмотрим функцию F(L, K) — сумма результатов битового сжатия всех численных последовательностей длины L с K чередующимися группами битов, которых, как мы уже знаем, C(L - 1, K - 1).
Для вычисления значения F(L, K) можно воспользоваться следующим подходом. Переберём размер t самой правой группы (младший двоичный разряд результата сжатия). Тогда легко получить следующее соотношение:
F(L, K) = sum(t = 1..L - 1) 2·F(L - t, K - 1) + is_even(K)·C(L - t - 1, K - 2) при L > 1; кроме того, F(1, K) = 0.
Для решения исходной задачи найдем сумму результатов числового сжатия для всех чисел X, меньших N + 1. Все эти числа можно разбить на несколько групп. Пусть в группу Gi попадут все числа X, у которых старший отличающийся бит от числа N + 1 стоит в позиции i. Обратим внимание, что это автоматически означает, что в X этот бит равен 0, а в N + 1 — равен 1. Для вычисления результата суммирования по числам из одной группы нам пригодятся результаты числового сжатия префикса N + 1 до позиции i и функция F(L, K).

Функция 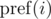 должна вычислить результат на префиксе числа N + 1, но только без учёта последней группы, если она содержит бит 0. Это связано с тем, что такую группу мы осознанно включаем в F(L, K).
должна вычислить результат на префиксе числа N + 1, но только без учёта последней группы, если она содержит бит 0. Это связано с тем, что такую группу мы осознанно включаем в F(L, K).
Описанное решение имеет трудоёмкость 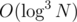 , но вы его можете ускорить до
, но вы его можете ускорить до 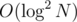 . Может даже быстрее?
. Может даже быстрее?
Задача E. Сборка велосипедов
Заметим, что в условии того, подходит ли нам четвёрка шестерней, можно заменить деление на умножение: четыре шестерни нам подходят, если их можно разбить на пары так, чтобы произведения диаметров в парах были равны.
Для каждого диаметра D посчитаем количество шестерней CD с таким диаметром, а также для всех возможных P посчитаем количество CntP пар, дающих произведение P. Это можно сделать либо за O(N2) с использованием контейнера HashMap / unordered_map или аналогичного, либо с использованием сортировки за 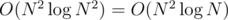 . Теперь рассмотрим все пары чисел. Для каждой пары шестерней с диаметрами D1 и D2 с произведением D1·D2 = P добавим к ответу CntP - 1: как количество "других" пар с таким же произведением. К сожалению, при этом, возможно, среди добавленных пар оказались и те, которые включают в себя шестерни, уже использованные в текущей рассматриваемой паре. Поэтому, если в текущей паре диаметры шестерней отличаются, то из ответа нужно вычесть CD1 + CD2 - 2, а если не отличаются, то (CD1 - 2)·2.
. Теперь рассмотрим все пары чисел. Для каждой пары шестерней с диаметрами D1 и D2 с произведением D1·D2 = P добавим к ответу CntP - 1: как количество "других" пар с таким же произведением. К сожалению, при этом, возможно, среди добавленных пар оказались и те, которые включают в себя шестерни, уже использованные в текущей рассматриваемой паре. Поэтому, если в текущей паре диаметры шестерней отличаются, то из ответа нужно вычесть CD1 + CD2 - 2, а если не отличаются, то (CD1 - 2)·2.
После этого у нас будут учтены все необходимые четвёрки шестерней, однако, к сожалению, по нескольку раз. Каждый набор из 4 шестерней вида D D D D (одинакового диаметра) будет учтён 6 раз, каждый набор вида D E D E будет учтён 4 раза, каждый набор вида D E F G или D E E F будет учтён 2 раза. Для того, чтобы это исправить, нужно для каждого диаметра D вычесть из результата 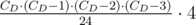 , для каждой пары диаметров D E вычесть CD·(CD - 1)·CE·(CE - 1)·2, и затем весь результат разделить на два.
, для каждой пары диаметров D E вычесть CD·(CD - 1)·CE·(CE - 1)·2, и затем весь результат разделить на два.
Задача F. Радары
Сначала рассмотрим случай, когда у нас всего одна контрольная точка. Ответ здесь тривиален: проще всего установить радар в точку, совпадающую с контрольной, и получить эффективность, равную 1.
Теперь рассмотрим случай, когда у нас две или больше контрольных точек. Пусть мы нашли ответ — расположение радара с наибольшей возможной эффективностью. Можно заметить, что мы можем перемещать радар относительно точки его расположения до тех пор, пока как минимум какие-то две контрольные точки не окажутся на целочисленных расстояниях от радара. Дальнейшее перемещение радара в любом из направлений, в результате которого любая из этих точек переходит через границу целочисленного радиуса, приводит к неувеличению эффективности радара (иначе наше предположение о том, что мы нашли расположение радара с наибольшей эффективностью, неверно).
Поэтому попробуем найти именно такое оптимальное расположение радара, при котором как минимум две контрольные точки лежат на целом расстоянии от него. Для этого переберём пару точек и расстояния r1 и r2, на которые эти точки отстоят от радара. Далее нам нужно найти точку на плоскости для размещения радара — это точка пересечения окружностей с радиусами r1 и r2 и с центрами в выбранных точках.
Таких точек может быть разное количество:
- 0, если окружности не пересекаются вообще,
- 1, если окружности касаются друг друга (в том числе внутренним образом),
- 2, если окружности пересекаются.
Для каждой точки пересечения окружностей посчитаем эффективность расположения радара в ней по определению и выберем глобальный максимум их всех таких расположений.
Итоговая сложность алгоритма получается равной O(N3·R2), где N — количество контрольных точек, а R — максимальный рассматриваемый нами радиус. Поскольку точки находятся в квадрате с координатами от 0 до 50, максимальное расстояние, которое вообще имеет смысл рассматривать, равно 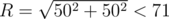 .
.
P.S. Если вы заметили опечатку сообщите мне об этом личным сообщением.











Сколько времени решение для Е работает на С++ ?
Авторское работает 1с.
Поделитесь с кодом, пожалуйста.
Вот мой АС на С#: http://codeforces.com/contest/675/submission/18054136 Вот еще есть хорошее решение ТЛЕ но на С++ он должен хорошо работать: http://codeforces.com/contest/675/submission/18054120
Мое решение отличается от авторского.
Can someone enlighten me why this code for E gets TLE? I have also tried with storing the diameter as a pair of integers but it didn't work, either.
Maybe it's because unordered_map is too slow. I was able to get AC (not TLE 26) only when I got rid of it.
Would you mind sharing your AC code? I did try to use map but it doesn't help.
I used approach, that differs from yours.
Here is my AC code. It uses sorting, but doesn't use maps at all
Try this test: http://codeforces.com/contest/673/submission/18055039 On Yandex system it is working 6.26s
Try reserving some space in the map upfront. If it grows up to O(n2), where n ≤ 4000, it's a lot of rehashing.
Thanks a lot! After reserving n2 buckets for the unordered_map, it takes 3.6s for the maximum test case.
Hi! Can you explain what "reserving some space in the map upfront" mean? How do I do that?
Use methods reserve or rehash
С E действительно как-то грустно получилось. Не так грустно, как на RCC, но всё же. Встроенный unordered_map получал TL, сортировка с ловербаундами зашла только после того, как стала сортировкой без ловербаундов :)
Ну или просто у меня руки плохо смонтированы.
O(NL) solution for A anyone ?
To solve this in O(NL), you maintain a freq[L][26], Here freq[i][j] stores the frequency of the ('A'+j)th character at the i-th position in the string. This frequency can be computed in O(NL). after that iterate the freq[][] array, and for each i, pick the maximum j, and use ('A'+j) as the i-th character.
I hope this solves it.
Let's find for each position the letter which appears on it in more than half of words, if none — every letter is ok. It is standart problem which can be solved in O(n) time for each position. Now I state that our word can differ from the right one no more than in one position. We can check the word in O(nL) time. If it is OK — great, problem solved. If it isn't then there is a word which differs from our in more than one position. We can change no more than one letter in our word, so that word differs in exactly two positions. Let's change letters in both positions and check these variants. Overall complexity is O(nL).
Code
Hey, I missed the contest, is there any link where I can see the problem set for this round ?
You can register here : https://contest.yandex.com/algorithm2016/contest/2498/enter/ And then start a virtual contest on the yandex site.
Can someone help me out with the O(n * 2^n) solution for Table Tennis Match, i.e. Problem C.