Hi there!
Is there going to be online-mirrors of Day 1 and Day 2?
Someone have info about this?
UPD: First online-version of IOI 2016 Day 1 will start on August 14, at 10:00 on https://contest.yandex.com/ioi/
UPD: Second online-version of IOI 2016 Day 2 will start on August 16, at 10:00 on https://contest.yandex.com/ioi/
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/25/2024 07:13:12 (f1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










As a beginner, online-mirror will not be very important for me, but my humble question is will IOI has online standing ?
thanks a lot and sorry for this annoying question.
EDIT: sorry I got it now, just ignore this comment
Mirror will be held on Yandex.Contest platform, link will be available on ioi website, contest.yandex.com/ioi, codeforces and more
day 1 result
Damnit, why so early. It also coincides with opening of the last problem of the current HR contest (which is the only one where time matters now).
It will be an open virtual contest — start whenever convenient
Oh. That's good, then. I'm too used to fixed times...
Will I get full feedback when I submit problem, or I must wait till end? I mean how many points I got for every subtask?
We'll try to keep things just as on IOI
I solved the first problem (detecting..) at o(nlogn) is there a solution at o(n)?
You can use two pointers to achieve O(N)
But, do not u need a sorted array?
i found an easy solution in o(N) time that uses only k smollest number algorithm and no sort
It must be like this, right?
it is the same but i didnt sort the array i took the first k numbers that ths sum of the first k is smaller then l and then sum of the first k+1 are larger then u the i took the smallest k and highest k and did the same as him and i also did the same thing with k+1
How to solve 2nd problems 3rd subtask?
no i am talking about the first problem, i wanted to know if the solution is o(n) time or o(nlogn) time
Did anybody submit successfully? I'm doing the contest now, getting CE with C++, it's saying that the function they're looking for in unidentified, although I followed their template for C (they don't have one for C++), should the function look differently for c++?
There is a download button in the upper right corner near "Jury messages" button. There you can find templates for different languages including C++.
Thanks
Does anybody know full solution (or something worthy of score over 71) for the last problem? I participated onsite and 71 is all I could get with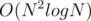 . cgy4ever explained a really cool solution for problem 2 in another blog, but I haven't seen anything about problem 3.
. cgy4ever explained a really cool solution for problem 2 in another blog, but I haven't seen anything about problem 3.
I haven't coded this but i think it should get 100. Label the nodes 1..N on the main line and 1'...N' attached to them, x[i] be the distance from 1 to i and l[i] be the distance from i to i'. Bsearch the answer, suppose the answer is <= t. Let u[i] = l[i]-x[i], v[i] = l[i]+x[i]. Let x1 < x2 be the "x-coordinate" (analogous to x[i]s) that we will add the extra edge between. Then for any i<j with u[i]+v[j] > t we need to have |x[i]-x1| + |x[j]-x2| + c + l[i] + l[j] <= t. This can be expanded into 4 different ineqs.
(x1+x2) — x[i] — x[j] + l[i] + l[j] + c <= t (1)
(-x1-x2) + x[i] + x[j] + l[i] + l[j] + c <= t (2)
(x1-x2) — x[i] + x[j] + l[i] + l[j] + c <= t (3)
(-x1+x2) + x[i] — x[j] + l[i] + l[j] + c <= t (4)
Note that inequalities (1) and (2) can be considered for all pairs i,j with u[i]+v[j]>t (not necessarily just i<j) without changing the system. Also (3) is tightest when i', j' are the diameter of the original graph so that can be precompd outside the bsearch. With some O(nlgn) precomp we can calculate max(-x[i]-x[j]+l[i]+l[j]) and max(x[i]+x[j]+l[i]+l[j]) over all u[i]+v[j] > t in O(n). We now have the tightest inequalities on (1),(2),(3) and we can now iterate through x1 and keep the interval of valid (satisfying 1,2,3) x2's using two pointers. We take the x1,x2 with minimum -x1+x2 as if anything satisfies the (4) ineqs then so will this one. Then check this answer by calculating the diameter for the resultant graph (possible due to special form) in O(n) to implicitly check all the inequalities of form (4). O(nlgAns + nlgn) overall, perhaps there's a simpler soln though.