Hi guys!
On IOI I've learned many new things, so now I want to give you a challenge. You probably remember my and Errichto's eliminations to VK Cup 2016. Let's focus on this problem: 674C - Levels and Regions
Main solution was solving it in O(n*k), because k wasn't greater than 50. What if k is just lower or equal to n? :D
Unable to parse markup [type=CF_TEX]
solution



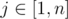 . Also, for fixed
. Also, for fixed 







I'm really interested if it's the first appearance of this nice idea on IOI?
You mean full solution of P6? Could you explain its solution. Couldn't understand Swistak's comment.
Well, I think it's not good idea to write it here. I can send it to you in PM.
I'll post solution in few minutes. :)
Trick to get from O(n*k) to O(n*log) is same in both tasks, so you can try to understand this one.
How to construct the answer in general case?
It was possible to use this technique in the problem 739E - Гоша выходит на охоту. In this problem there could be a case where res(k + 1) - res(k) = res(k) - res(k - 1) where k is the value that we are looking for. This implies that there is no real value X which selects exactly k things. It is still quite easy to find the value of the answer by using this technique. However constructing the configuration that gives the answer seems to be really hard and I can't figure out how to do it. Does anyone know a general way to construct the answer when using this technique and the function is not strictly convex?
Hello,
Can anyone explain this method in other words, I can't fully get the idea. in particular, what is res(i)? is it optimal solution when K=i ? if yes then res(i + 1) - res(i) should be negative because of observation 1. also how could those observations imply " res(i) + i·X ≤ res(j) + j·X " ?
How did you prove res(i + 1) - res(i) ≤ res(i) - res(i - 1)? Radewoosh
Consider some partition of [1, n] into M disjoint intervals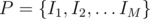 , and define
, and define 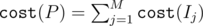 . Let P * M be a partition that minimizes
. Let P * M be a partition that minimizes  over partitions with M elements. Then we define
over partitions with M elements. Then we define
(and for partitions that aren't optimal over their number of elements, we set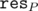 to 0 everywhere).
to 0 everywhere).
Then each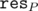 is convex, and
is convex, and 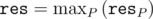 is also convex.
is also convex.
EDIT: Wow, this is completely wrong -- I have magically managed to show that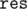 is convex, but it was supposed to be concave!! It isn't hard to fix; if you switch to a more natural definition of
is convex, but it was supposed to be concave!! It isn't hard to fix; if you switch to a more natural definition of 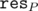 (for a partition into M parts -- optimal or otherwise):
(for a partition into M parts -- optimal or otherwise):
then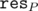 is concave (and not convex like I said earlier -- oof), and
is concave (and not convex like I said earlier -- oof), and 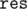 is the min over all
is the min over all 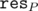 .
.