Hi everyone, here are the solutions to the contest problems.
Note that a[i] + a[i + 1] = b[i]. Use the initial condition b[n] = a[n] and we can figure out the entire array b.
Time Complexity: O(n)
First, if S has odd length, there is no possible string because letters must come in opposite pairs. Now, let's denote the ending coordinate after following S as (x, y). Since S has even length, |x| has the same parity as |y|. Suppose they are both even. Then clearly, we can make x = 0 in exactly  moves, and same for y. If instead they are both odd, then we can change exactly one x-character into a y-character. With the correct choices of these characters, now our string has |x| and |y| with even parity, thus reducing to the problem above. Therefore, the answer is (|x| + |y|) / 2.
moves, and same for y. If instead they are both odd, then we can change exactly one x-character into a y-character. With the correct choices of these characters, now our string has |x| and |y| with even parity, thus reducing to the problem above. Therefore, the answer is (|x| + |y|) / 2.
Time Complexity: O(|S|)
712C — Memory and De-Evolution
Let's reverse the process: start with an equilateral triangle with side length y, and lets get to an equilateral triangle with side length x. In each step, we can act greedily while obeying the triangle inequality. This will give us our desired answer.
Time Complexity: O(log x)
One approach to this problem is by first implementing naive DP in O((kt)2). The state for this is (diff, turn), and transitions for (diff, turn) is the sum (diff - 2k, turn - 1) + 2(diff - 2k + 1, turn - 1) + 3(diff - 2k + 2, turn - 1) + ... + (2k + 1)(diff, turn - 1) + 2k(diff + 1, turn - 1) + ... + diff( + 2k, turn - 1).
Now, if we use prefix sums of all differences in (turn-1), along with a sliding window technique across the differences, we can cut a factor of k, to achieve desired complexity O(kt2).
However, there is a much nicer solution in O(kt log kt) using generating functions(thanks to minimario). We can compute the coefficients of  , and the coefficient to xi corresponds to the number of ways we can form the difference i. To compute these coefficients, we can use the binomial theorem.
, and the coefficient to xi corresponds to the number of ways we can form the difference i. To compute these coefficients, we can use the binomial theorem.
Time Complexity: O(kt2)
Time Complexity: O(kt log kt)
Lets think about two segments of casinos [i, j] and [j + 1, n]. Let L([a, b]) denote the probability we dominate on [a, b], and let R([a, b]) denote the probability we start on b and end by moving right of b. Let
l1 = L([i, j]),
l2 = L([j + 1, n]),
r1 = R([i, j]),
r2 = R([j + 1, n]).
You can use a geometric series to figure out both L([i, n]) and R([i, n]) using only l1,l2,r1, and r2. To derive these series, think about the probability we cross over from j to j + 1 once, twice, three times, and so on. The actual formulas are,
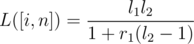

Now we can build a segment tree on the casinos, and use the above to merge segments.
Time Complexity: O(N + QlogN)










Can someone explain how to solve D using generating functions as mentioned in editorial ?
Auto comment: topic has been updated by send_nodes (previous revision, new revision, compare).
Could someone elaborate solution to D ? Didn't really understand it. How is the equation formed ?
The equation is divided by x^k, so actually the exponents of x are from -k to +k, and when raised to 2*t, coefficients of x^i will give the number of ways in which 2*t numbers between -k to +k will add up to i.
And for Memory to win the final score should be greater than b — a, so we are interested in sum of all the coefficients whose exponents are greater than b — a.
Can you explain the code , as far as I know we can solve the numerator as a geometric series , then the coefficients in denominator can be easily found but for the numerator I have not seen a method better than exponential in the number of brackets
For C, does anyone have a formal proof that greedy is okay? I had some intuition that's a very handwavy proof, but I don't have a formal proof of correctness. In general, I find that proving greedy algorithms will work is tricky.
The minimum side is a bound for velocity of increase.
This thought was one of the two basis of my intuition, but it's not a formal proof at all.
Which part in particular did you failed to convince yourself that the greedy algorithm must be true?
It is interesting that, reversing the problem reduces the problem complexity to a lot than it sounds.If anyone with a greedy solution without "reversing approach" is most welcome.
Proof regarding the approach mentioned here, Lets set (x,y,z) be length at any step.
When I read the problem statement, This idea didn't strike me. Reversing is too powerful tool here I think.
This is more or less how my intuition went, but it's not a formal proof at all. Your statement "substituting maximum velocity obviously minimizes the steps taken", is extremely hand-wavy. You could say something similar for many kind of problems where greedy doesn't work. For instance, in the coin changing problem: https://en.wikipedia.org/wiki/Change-making_problem
it's well known that greedy isn't optimal for certain coin denominations, yet you could say "maximizing the amount you take away obviously minimizes the steps taken" which is a completely wrong statement, but in my view, quite analogous to your argument here.
Intuition should be enough here because you can just reverse all your steps and it makes pretty good sense.
Alternatively you could also write a brute force, and then just check it yourself.
Here is a more detailed write-up of the proof that the greedy algorithm works. As in the explanation, we start with an equilateral triangle with side length b and must get to one with side length a ≥ b.
Proof. Call a triple (x, y, z) valid if x ≤ y ≤ z and x + y > z. In other words, a triple is valid if it is sorted and corresponds to the side lengths of a non-degenerate triangle. We will say (x1, y1, z1) ≤ (x2, y2, z2) (with ≤ read as "dominated by") if x1 ≤ x2, y1 ≤ y2, and z1 ≤ z2.
Suppose we have (x1, y1, z1) ≤ (x2, y2, z2) ≤ (a, a, a) with all triples valid. We show that (x2, y2, z2) can reach (a, a, a) in fewer steps than (x1, y1, z1) when using an optimal algorithm. To see this note that any sequence of side increases valid on the smaller triple can also be applied to the larger triple. More specifically, suppose we wish to increase x1 → c. Then we can increase x2 → max(c, x2) with the modified triples (once sorted) still both valid and in the same domination order (requires a little checking). The same can be seen for modifying y1 or z1. Since the domination order remains respected, the increases can be repeated inductively until reaching (a, a, a).
Starting from any valid triple (x, y, z), we finally note that the side increase to (y, z, y + z - 1) gives a valid triple that dominates all other possible valid triples achievable with 1 increase. To see this first consider increases in z → c. Then c ≤ x + y - 1 and we have (x, y, c) ≤ (y, z, y + z - 1). If instead we increase y → c then we either have (x, c, z) ≤ (y, z, y + z - 1) or (x, z, c) ≤ (y, z, y + z - 1). Lastly, if we increase x → c we either have (c, y, z), (y, c, z) or (y, z, c) all of which are dominated by (y, z, y + z - 1).
Thanks. Aside from the minor issue that you didn't prove you should never decrease your edge, I think this is a complete proof.
Nonetheless, I'm a bit perplexed that so many people solved this question during the contest. I did too, but only because I kinda gave up on proving its correctness and hoped my intuition was correct... I imagine most people did what I did which kinda makes this problem bizarre in that in punishes people who are more careful than me (I believe something they should be rewarded for). I think such questions aren't good for contests as it encourages just random stabs at a solution (which you would never do in real life).
For Problem D, See my O(kt^2) implementation. Here
Main idea : dp(t,i) can be calculated easily using dp(t,i-1) and dp(t-1,i+k) and dp(t-1,i-k-1).. See , dp(t,i) and dp(t,i-1) has much in common.
here dp(t,i) means # of ways to achieve i, after t rounds.
Can u please clarify ur recurrence relation,especially the transition of dp(t,i) from dp(t,i-1). Thanks in advance.
Let dp[i][j] be in how many ways you can achieve difference j in i turns.
1.dp[0][0] = 1.
2.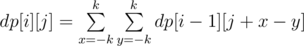 .
.
You can easily check that dp[i][j] = dp[i - 1][j - 2k] + dp[i - 1][j - 2k + 1] × 2 + ... + dp[i - 1][j - 1] × 2k + dp[i - 1][j] × (2k + 1) + dp[i - 1][j + 1] × 2k + ... + dp[i - 1][j + 2k - 1] × 2 + dp[i - 1][j + 2k].
Finally to get an O(kt2) solution you can see that:
Here is my implementation.20514640
How did you simplify from 2nd last equation to last equation ??
Try to find dp[i][j - 1] - dp[i][j] using the third relation.
dp[i][j - 1] - dp[i][j] = - (dp[i - 1][j - 2k - 1]) × (1 - 0) - (dp[i - 1][j - 2k]) × (2 - 1) - ... - (dp[i - 1][j - 1]) × (2k - (2k - 1)) - (dp[i - 1][j]) × (2k + 1 - 2k) + (dp[i - 1][j]) × (2k + 1 - 2k) + ... + (dp[i - 1][j + 2k]) × (2 - 1) + (dp[i - 1][j + 2k + 1]) × (1 - 0)
I tried to implement your formula but it gives me some negative intermediate result. With
dp[i][j] = dp[i][j-1] - sigmaA + sigmaB, I found that there are cases wheresigmaA > sigmaBsodp[i][j]goes negative. Is my implementation wrong 'causesigmaA > sigmaBwill never happen technically or do I need special treatment for this case?http://codeforces.com/contest/712/submission/20563138
If sigmaA < sigmaB add sigmaA - sgmaB + MOD otherwise sigmaA - sigmaB.
ans += (dp[now][i + shift] * pr[max(0,o+shift)]) % MOD;Can you tell me what this line means? Why we need to multiply dp[][] with pr[]?
In questions C without reversing the question and decreasing the side instead of increasing, we can still solve the question greedily, right?
What advantage is reversing the question giving us?
The advantage of reversing is that it let us know the max possible value to increase. You just do something like this: a = min(x, b + c — 1).
And how can you solve the problem without reversing? My attempts have failed.
Notice that something like a = max(y, c — b + 1) didnt' work — it can't take us the best answer, you can check it out even in example x = 22, y = 3.
D can be solved with Inclusion–exclusion principle in
O(Kt^2).we can calculate how many way to get X scores in
O(t), and all possible scores inO(Kt^2), then we can easily get the answer.see Submisson
why this(http://beepaste.ir/view/e6b2016b) doesn't work?? I simply added k to everything ... I don't get why using Inclusion-Exclusion principle :(
Really beautiful way! If anyone stumbles upon, the inclusion-exclusion here is by number of steps in which we add >2*k points.
Can anyone explain O(ktlogkt ) approach for problem D?? In,particular how to get expression for pref2[i]??
i am getting runtime error on test case 15. but i am not able to see test case.can anybody help here is submission link:submission
When will be the test cases be visible. I am getting runtime error on test 15 for Div2D. The solution is a simple 0(k^2 . t) top-down dp carrying differences of score with an offset. Need some help with this. My Code Thanks in advance.
Isn't your array a little bit to small? At most there are 2*k*t+100 points difference between the two players, I believe that is larger than 1e4.
Well thanks for pointing that out , now after I corrected that mistake , and also reducing the time complexity to O(KT) , the solution is giving Time limit exceeded on test case 15. Can you point out the mistake. Where am I going wrong. 20525457
Your solution does not work in O(KT).
There are O(K*T) states for each turn of the game, and a total of O(K*T*T) states for the whole game, and you're taking O(K) time to compute each state of it, so that's O((KT)^2) in total.
The editorial have mentioned two ways of optimization. Both of them fits in the time limit, feel free to use the one that you are comfortable with. The first approach is about the sliding windows technique and prefix sum, and the second approach is about divide and conquer with an observation on the binomial coefficients.
here is my submission for problem D use partial sum 20521519 . One loop I use about 4 * 2 * MAXSCORE. Total operation ~ 800000 * t (don't contain +mod or -mod) and runtime is 200ms. CF is very fast !! PS: My source code use tab 2 and when I submit it is hard to read. How can I fix it? sorry for my bad English
Can someone explain me C in more detail, please.
Can someone please elaborate on the explanation of E.
*It is strongly advised to pick up your pen to do a little math to understand the solution better.
I will used the same terms that the editorial uses, L[a,b]= probability dominating from a to b while starting from casino a, R[a,b]= probability of starting from casino b and ending up at casino b+1 without losing at casino a. (The editorial missed out the never losing at casino a part)
From the definitions we can find out the merging formulas of L&R[a,b] and L&R[b+1,c] (a,b,c, in range of n), c does NOT NECESSARILY needs to be n.
For L[a,c], it's a GS sum of L[a,b]*L[b+1,c] (note that L[a,b] makes Memory ends at b+1) + L[a,b] * (1-L[b+1,c]) * R[a,b] + ... (If Memory fails to dominate on interval [b+1,c], then multiply R[a,b] to get him back to position b+1), from the GS sum formula you can end up with a similar formula as shown in the editorial.
For R[a,c], it's a sum of two parts. The first part is R[b+1,c], this is pretty obvious. The second part is the GS sum when Memory fails at casino b+1 but never fails at casino a. The first term of the GS is (chance of failing at casino b+1) * (chance of getting back to b+1 w/o failing at casino a) * (dominating on [b+1,c]), that is (1-R[b+1,c]) * (R[a,b]) * (L[b+1,c]). The ratio of the sequence is (chance of failing to dominate on [b+1,c] = 1 — L[b+1,c]) * (chance of getting back to b+1 w/o failing at casino a = R[a,b]). That also brings us to the formula that the editorial gives.
My implementation: http://codeforces.com/contest/712/submission/20521550
*In case if you don't know understand segment tree, go to learn it before reading this code.
Can someone explain in Problem D, How's total number of games played will be (2*k+1)^(2*t) ??
Can someone clearly explain how we can get the formulas in problem E?
Let's solve case, when (l, r) = (1, n), and there are no modifications:
Consider a walk on casinos 0, 1, 2, ..., n, n + 1 (0 corresponds to a state "lost in casino 1", n + 1 corresponds to "won in casino n").
Denote fi = "the probability to get into casino n + 1, if we're in casino i", i = 0, 1, ..., n + 1, Δi = fi - fi - 1, i = 1, 2, ..., n + 1,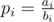 , and
, and 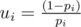 .
.
We know that f0 = 0, fn + 1 = 1, and fi = (1 - pi)·fi - 1 + pi·fi + 1 (i = 1, 2, ..., n). We need to calculate f1 = Δ1 (a.k.a. solve system of linear equations).
Rewrite this equation as fi - fi - 1 = pi·(fi + 1 - fi - 1), rewrite using Δ to get Δi = pi·(Δi + 1 + Δi), rewrite again and this becomes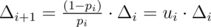 .
.
Remember that Δ1 + ... + Δn + 1 = (f1 - f0) + ... + (fn + 1 - fn) = fn + 1 - f0 = 1, so Δ1(1 + u1 + u1·u2 + ... + u1·u2·...·un) = 1, and finally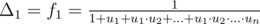 (formula for f1 that we were looking for)
(formula for f1 that we were looking for)
Segment tree:
General case (note: in segments I store quantities different from those in authors solution)
for segment [L, R] store values A[L, R] = (uL·uL + 1·uL + 2·...·uR) and B[L, R] = (uL + uL·uL + 1 + uL·uL + 1·uL + 2·... + uL·uL + 1·...·uR).
Recalculate them like this: A[L, R] = A[L, M]·A[M + 1, R], B[L, R] = B[L, M] + B[M + 1, R]·A[L: M].
The answer for [L, R] will be .
.
I'm also not sure, why the constraint pi ≤ pi + 1 was given, I (probably) only used the fact that pi ≠ 0.
It was given becauze consider a test case of 50000 casinos with probability (1 — 1e-9) followed by 50000 casinos with probability 1e-9. Answer over whole interval should be 0.5(I think), but precision will make it 0.
How would one prove that something "bad" (imprecision due to overflows) wouldn't happen with condidion pi ≤ pi + 1?
Thanks for explanation. I couldn't get the editorial from the post :(
For E I used sqrt decomposition with the following idea:
Let D(l, r) denote probability to dominate on [l, r]
if l = r, then D(l, r) = ar / br
else D(l, r) = pl * (D(l + 1, r) + (1 - D(l + 1, r)) * D(l, r))
The idea is simple: if at beginning, we move to left at l (probabilty (1 - pl), we lose.
So now we've moved from l to l + 1, and there are two cases: Either we dominate in (l + 1, r), or we move left (thus don't dominate) and return back to D(l, r).
So we can compute D(l, r) from D(l + 1, r) like this transform:
D(l, r) = D(l + 1, r) / (D(l + 1, r) - 1 + 1 / pl)
Since D(l, r) are fractions, represent them as a 2x1 vector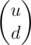 denoting
denoting 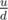
And we see that if we apply the above transform, it's just multiplying matrix by vector and getting a new vector.
Now just build a sqrt decomposition or a segment tree to quickly get matrix multiplication for segments and multiply it by pr.
Submission http://codeforces.com/contest/712/submission/20531915
Can you please elaborate more on how you join results from the various sqrt segments.
i.e How to do D(l,r) given D(l,k) and D(k+1, r)? Given the definition of dominate, I am not sure how just multiplying these two would work.
Also how did you come up with this: "Given D(l,r) are fractions represent them as 2x1 vector"..
I treat fractions as vectors
as vectors 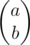
So we have the formula
D(l, r) = D(l + 1, r) / (D(l + 1, r) - 1 + 1 / pl)
Let's shortcut it as following:
D(l, r) = Fl(D(l + 1, r))
Here Fl is a transform that takes D(l + 1, r) as input and outputs D(l, r)
D(l, r) = Fl(D(l + 1, r)) = Fl(Fl + 1(D(l + 2, r)) = Fl(Fl + 1(Fl + 2(D(l + 3, r))) = ... = Fl(Fl + 1(Fl + 2(Fl + 3(... Fr - 1(D(r, r))))))
Let's see how Fl acts on fractions
After simlplifying we get
So we see that Fl takes a fraction and transforms it into another fraction, whose coefficients are linear combination of source coefficients.
This can be written like this:
Let's call this Fl operator matrix Ml and let C(l, r) be D(l, r) represented as a 2x1 vector corresponding to its fraction. E.g. if D(l, r) is , C(l, r) will be
, C(l, r) will be 
C(l, r) = Ml * Ml + 1 * ... Mr - 1 * C(r, r)
So all we need is to know how to quickly compute product of matrices on a segment. Use segment tree or sqrt decomposition for this.
Also this solution doesn't seem to use the knowledge that pl is non-decreasing in any way. — Oops, this is false, this is actually needed since otherwise we would lose too much precision,as described here: http://codeforces.com/blog/entry/47050?#comment-314304
Have a look at these two submissions for problem D: 20533661 20534239
The first one fails on test 17, but the other gets AC. The only difference is changing the shift length and the limit. Why is this? I thought I checked whether or not the space was large enough already, and even now I'm not sure why it was a problem.
After t turn the minimal difference will be - 2 × t × k and the maximal will be 2 × t × k so you need 4 × t × k + 1 positions.
Also if you want to have negative indices you can do it with this trick:
I used this in my submission.20514640
Nice trick, by the way. I think I understand where I went wrong now. Thanks.
Probably there is solution for D which uses fact that after multiple convolution we get very close to normal distribution...
What?
Hi, for problem C, can someone explain
Why does counting down give a separate answer as compared to counting up?
Greedy Approach
Example
22 to 4
22,22,22 -> 22,22,4 -> 22,19,4 -> 16,19,4 -> 16,13,4 -> 10,13,4 -> 10,7,4 -> 4,7,4 -> 4,4,4
4 to 22
4,4,4 -> 4,4,7 -> 4,10,7 -> 16,10,7 -> 16,10,22 -> 16,22,22 -> 22,22,22
why counting up gives us the solution? (proof for correctness)
I was thinking of a DP solution for it(counting down). Is it a special case, where the optimal solution of a subproblem same as the greedy solution?
Counting down means moving from 22 to 4.
Counting up means moving from 4 to 22.
I guess divergence of this process is faster than convergence, that's why.
Let's look at divergence rate, (y,y,y) to (x,x,x):
Take the smallest, and set it to sum of other two-1.
1. Clearly, as long as at least one of the other two is larger than the smallest, the number is multiplies by a real factor of at least 2.0. The only case when the smallest is multiplied by a factor < 2.0 is when all three sides are equal.
We can prove that only happens when all three sides are = y. This is because when we set the smallest to sum of other two-1, we are guaranteeing that this value becomes larger than both the remaining sides(with exception of side=1, which is outside our constraints). Now, from point (1.) we know that we are effectively taking at most log(x/y) steps, as y*(2^steps) >= x.
Let's look at convergence rate, (x,x,x) to (y,y,y): In the first step, set one of the numbers = y. Then, Take the largest, and set it to absolute(difference of other two) + 1.
Therefore, in second step, we have set the largest value = x-y+1.
In third step, we have set the largest value = x-y+1-y+1 = x-2*y+2.
In fourth step, we have set the largest value = x-2*y+2-y+1 = x-3*y+3. and so on.
Thus, total number of steps = 1 + x/(y-1).
Solving for 1+x/(y-1) <= log(x/y) keeping y constant (c = y-1)
x/c <= logx — log((1+c)*2) where c>=2 (constraints)
Using z = x/c
z <= log(z) -log((1+c)*(2*c)). So, never.
Another way of checking for 1+x/(y-1) <= log(x/y)
y=3 : x/2 <= log(x/6) => never
y=4 : x/3 <= log(x/8) => never and so on.
Therefore, rate of divergence is always more than rate of convergence.
I just solved Problem E with two segment trees, just like the official solution. But I still don't know why the problem needs the condition that the probabilities are in non-decreasing order. Even I solved without using that condition and got AC. Is it just a fake condition?
So that precision errors dont occur. Look at caze with 5e4 casinos probability (1-e-9) and 5e4 casinos probability (e-9). Precision will give you a very different answer than actual
oh I see. thx
Can someone explane me solution in complexity O(k t log kt) for fourth task in more details ?
I solved task in the first complexity and that is not problem, but I can not understand how we generate polynom from the solution and why coefficient near xi is equal to DP [ t ][ i ] ?
The problem is actually more mathematical than DP-ish. Start from the value 'a'. There are 2k+1 edges going out, and so on for the further levels. This gives us binomial pyramid like structure. Simply apply formula for last level only.
In case you are asking about the formula itself, I haven't worked it out yet. There's a comment about solving with inclusion exclusion. Maybe you can check it out as well. :)
Hi every one , for problem D I didn't hear about sliding window technique before , so i read about it and i got a shallow idea about it, but still not unerstood how we can use it here , i didn't understand anything about that, reading the editorial and the implementation .
can any one help me with details. thanks in advanse.
Can you prove the greedy approach for Div2C , during the contest I first thought of doing greedily from larger sided triangle to smaller one , obeying triangle inequality , which was incorrect. But the doing the same thing from smaller to larger passes.
There are 2 comments above which try to prove it. here's my attempt to prove it. Have a nice day.
Can someone explain to me the problem statement of E? What is a valid walk here? We can never go left of i but we can go right of j? Also, why is the statement given as
Note that Memory can still walk left of the 1-st casino and right of the casino n and that always finishes the process.if we can never go left of i?Please help.
A walk is you can go wherever you want, including left of i and right of j. A valid walk, however, means you can't move left of i and you must walk right of j to finish the process.
So, as soon as I walk right of j, is my walk over? Or can I go right of j as many times I want, but I have to return to j and then win in order to finish my walk?
Walk ends the first time you go right of j.
Thank you :)
I found myself trapped in some kind of (seemingly) paradox in problem E.
For each position i, we can get a probability pr[i] for returning to position 1. Obviously, pr[] is non-decreasing. Now there is a problem. We have 1-pr[i] probability to go back to position 1, but pr[i] is definitely not the probability you can get to destination (it is just the probability to get to i+1). However as the procedure is infinitely repeated until getting to the destination(on either side), so outside 1-pr[i] we must reach the other end.
Where is my fault in reasoning?
Hey guys,
Can anyone please take a look at my solution to D and suggest any improvements. It gets accepted and it seems to be running quite fast but I would like to improve it :)
http://codeforces.com/contest/712/submission/20639410
Can you please explain why the in the transformation (diff, turn) = ( diff — 1 , turn — 1 ) + 2 ( diff — 2*k + 1 , turn — 1 ) + ........ Why we are multiplying by 2, 3 here?
To get diff-2*k, there's only one way since both players need to get -k. To get diff-2*k+1, there's two ways since players can get -k and -k+1 or -k+1 and -k, respectively, and so on. You can see it's like a dice roll probability distribution with the peak at 0.
Got that. Thanks a lot.
can not understand the solution. if at current turn, both player get -k , then their new difference should not be diff+(-k-(-k))=diff+0 ??
I believe D can be solved using an easier version of prefix sums.Just calculate number of ways to get a particular score after t turns for a person, then final answer is just the appropriate convolution of the score combinations which can again be done with the already calculated prefix sums.