I'm sorry for a delay with publishing the editorial.
Tutorial is loading...
Problem author: MikeMirzayanov.
Tutorial is loading...
Problem author: MikeMirzayanov, Kniaz.
Tutorial is loading...
Problem author: MikeMirzayanov.
Tutorial is loading...
Problem author: MikeMirzayanov, Kniaz.
Tutorial is loading...
Автор задачи: Kniaz.
Tutorial is loading...
Автор задачи: MikeMirzayanov.
I want to thank Mikhail Piklyaev (awoo) for translation of tutorial!










What about the problems E and F?
I think they should be published soon. You can also ask me if you would like some tips!
Can anyone explain C and D in a simpler language? That would be a great help. Thanks in advance!
I am not sure about the approach of C in the editorial, but here's my O(n) approach:
Observation: a[] can be converted into b[] by grouping a[] in non-overlapping segments.
If we start from the left, it is obvious that the answer exists only if the prefix sum (the sum of the first few elements) is equal to b[0] since a[] only consists of positive numbers. This fact could also be inducted to other segments if we consider that previous segments were cut away from a[] and treat the next element as the start of the segment for b[1...n].
Now the only thing we have to care is whether the monster could start the momentum by eating others. By greedy we will assume that we are starting the eating processes of each group from the largest monster (as there are no non-positive elements), if you can't start the eating process (note that the eating process is only needed when the size of the group is larger than 1).
Remember to store the correct positions of the monster during the eating process as the editorial has mentioned.
The editorial for D pretty much nailed it and I don't think my explanation could beat that. Perhaps you should take a look at other's code.
For problem C:
You should select one largest monster which isn't surrounded by two equal monsters.
To avoid being bothered with changes of position, you may process from the last block to the first block.
Check my code: 21929693
Assuming you have the largest monster, how do you know whether to delete to the left or to the right? And how many elements to delete?
You should check and store min neighbour for current giant monster. See "getNeigh" function:
http://codeforces.com/contest/733/submission/27457231
haleyk100198 can you tell me the mistake in this solution 93391656 of Problem C(DIV2)[contest:378][problem:Epidemic in Monstropolis] THNAKS IN ADVANCE.
How to solve C in O(n)- challenge ?
Like this. 21968223
Not very different than what is explained in the editorial. For a group S that needs to get reduced to one monster, find a monster which has maximum value and doesn't have an equal neighbour(if there is no such monster, then no solution). Once he eats this unequal neighbour, he can eat everything else in any order. So you'll either eat everything to the left and then everything to the right, or eat everything to the right and then everything to the left. And this way it's easy to keep track of his position in the final array, without simulating the transformations on the array.
try to use two pointers one starting at first of 1st array and other at start of 2nd array.
first time traverse whole b array to check if solution exists.if doesnt exist print NO and exit
else if yes traverse again second time through 2 nd array and print the solution.
for printing the solution,follow a greedy approach finding the maximum in it and assume it eats all the others in that union
here is the link to my solution of it:http://codeforces.com/contest/733/submission/21949174
Ooops.. looks like my solution was incorrect. Took us a while to figure it. Sorry to everyone who wasted time trying to figure it out. I'll think more carefully next time.
Check the last edit if you wanna read the incorrect solution.
Can you prove its correctness? I'm not sure about this.
I presume you are suspicious that the Kruskal is incorrect, now that edges change their initial values?
Indeed, I see that I wasn't rigorous enough about it. Looking over the Kruskal proof, you can make it still hold if edges that you haven't added yet to the MST can only increase in cost during the algorithm(which is what happens in my algorithm. The edges of category 2 increase in value until they reach category 1, but we fix their cost if we add them to the MST before that).
Later Edit: No, it doesn't work.
Hi Mikester, I understood the following.
For a tree with n — 1 edges, the dissatisfaction will be Sum(w(i)) — S/c where c = minimal weight of edges in the tree.
Now, if I fix c, which is equal to weight of some edge, I need to minimize sum(w(i)), that is find the minimal spanning tree containing edge with the weight c and all other edges have weight >= c.
Can you explain after that point? I mean how do I optimize it?
Hmm, looks like I am close to the solution
http://codeforces.com/blog/entry/9570
I can't understand what exactly are you representing with extra[i] array.Can you please elaborate a bit?
extra[i]is in this instance of the problem-S/c[i]It's incorrect. consider following case
4 4
0 0 1 10
100 100 5 1
1 2
1 3
2 3
2 4
10
your solution gives sum 1 and selects edge 3, 1, 4, but the optimal solution should give sum 0 and select 1 2 4.
Wow, you're right.. Good job! I thought I had a cool insight about Kruskal too. What I said about it was incorrect. My apologies.
Implementing E was really painful, and had so many errors. Finally felt peaceful after getting AC. After seeing many people using binary search, I thought that I was making the problem very hard for myself but it seems that the editorial explanation is exactly what I have done(not sure). I considered all the cases separately in query function, and always made sure that when I am calculating the answer for s[i], it is always U. Otherwise I find the answer in the inverse string, where it would be U.
What's the approach using binary search?
I have a (possibly dumb) question about Problem F: Why would it be optimal, given a fixed selection of main roads, to reduce the dissatisfaction value of just a single road? Would that still hold if the budget is not divisible by the unit repair cost of the selected road? In that case, would it be more optimal to distribute the budget over multiple roads whose total repair cost could make better use of the budget?
That's a dumb question indeed :P . What you are saying is like this .. 19/3 can be greater than 15/5 + 4/4 . just because you are using all the money it doesn't provide you with more number of dissatisfaction units(because the cost is also high). Mathematically it goes like this.. a*x + (a-1) = Sigma(Bi*Yi). where each Bi is greater than 'a' implies Sigma(Yi) <= x. It's easy to prove :) . However my submission was giving wrong answer on test 75. can anyone please check ? what's special about testcase 75? here's my submission- [submission:21965336]
Even if
S % c[i] != 0,floor(S/c[i])is maximized whenc[i]is minimal.There's a simple argument: Assume you allocate some budget to road
jsuch thatc[j] > c[i]. Note that this budget could be moved to roadiat no loss (indeed, possibly at a gain).Thanks @Artemis_Fowl and @OMGTallMonster for explaining! That was indeed dumb.
I was also confused about that one.
The OP says that fix an edge to be reduced and find MST corresponding to that edge.
Now, it would be correct if the cost of that reducing edge was minimal. But what if there was an edge with smaller cost of reducing in that same spanning tree. Then we could reduce the dissatisfaction by reducing that edge. So I thought this, fix a road, find a MST containing that road, where all edges have cost of reduction >= c, where c is the cost of reducing dissatisfaction of the edge we initially chose. But it turns out I don't have to do actually that. What we need to do is that if there are multiple spanning trees of the same weight, then for all those spanning trees, we should choose the tree containing the edge with smallest reducing cost. So, we select an edge P, find MST corresponding to that edge. Suppose w(P) > w(Q) (w(p) = cost of reducing dissatisfaction of the edge p) for some other edge in the MST, then we know that MST(P) >= MST(Q)(either MST(P) = MST(Q), or at least one edge is different with smaller weight, so MST(Q) < MST(P) ), therefore we know that when we finally find MST corresponding to Q, the answer is obviously better and hence no need to find MST with weight >= c.
Really liked the problem C.
Need more problems like this.
I didn't think that it would be that easy.
Problem F should add this case:
5 6
3 3 3 3 4 9
100 100 100 100 2 1
1 2
2 3
3 4
4 5
1 5
1 5
7
The answer is 10. But my solution got 11 and passed all system test cases.
problem F : Precalc takes ? or
? or 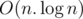 for Binary lifting ?
for Binary lifting ?
O(nlogn)
Thank you for such intersting problemset! The problems(especially E and F) worth thinking & solving :)
Can someone help me in finding the bug in my submission for problem C . I followed the same approach in the editorial but I'm getting a WA at test 64 . The checker comment is Wrong answer Can not eat not less . Since it's a large input I couldn't find the bug.
I would be very thankful if someone could help me out.
My submission with comments : LINK
UPDATE : I managed to find the bug and solved it.
I think I'm missing something in the complexity argument for F. How do you add an edge to a tree and delete some edge in the cycle without paying O(m) to reverse the links in the path between the added edge and the deleted edge? (The links are directed, and thus must be reversed, based on the LCA binary lifting article elsewhere in the blogs.) Which would raise the total time complexity to O(n log n + m^2).
Example: Tree rooted at A, with a child B. C is a descendant of B at depth O(m) [since this is an unbalanced tree]. Leaf D with depth O(m), not in B's subtree. Need to add an edge between C and D: LCA is A; suppose the heaviest edge in the cycle is (A,B). Then we need to reverse links on path B..C with total cost O(m).
You don't have to do the whole operation. Instead, you just find the LCA to identify the unique cycle that will be created in log time, and then use binary lifting to identify the best edge to be removed.
(When you create the binary lifting lookup table, you lift it in the way that the edges are directed to the parents, that's the way you want to do it anyways, you don't need to reverse it everytime you lookup the table then.)
Can anyone prove the correctness of given solution for F ?