Приветствую всех участников раунда!
203A - Две задачи
Из-за совсем небольших ограничений можно было перебрать минуту, на которой Вася пошлет решение по первой задаче и минуту, на которой Вася пошлет решение второй задачи. Однако были несколько хитрых случаев: нужно было не забыть, что Вася может послать только одну задачу (то есть в этом случае нужно было перебрать только одну величину), а также может вообще не посылать задачи — в этом случае он получает 0 баллов.
203B - Игра на листочке
В этой задаче очевидно следующее тривиальное решение: после каждого хода нужно проверить, не появилось ли черного квадрата со стороной 3 на поле, но ограничения не позволяют так решать задачу. Однако заметим, что как только Вася закрашивает некоторую точку (x, y), то требуется проверить лишь 9 возможных кандидатов на черный квадрат, а остальные квадраты со стороной 3 не поменяют своей раскраски.
Таким образом, решение работает за O(m) с константой порядка 80 и требует O(n2) памяти.
203C - Фотограф
Заметим, что если Вася хочет обслужить клиента номер i, то ему понадобится ровно f(i) = a·xi + b·yi мегабайт памяти на фотоаппарате. Также заметим, что так, как мы хотим максимизировать количество клиентов, то гораздо выгоднее брать тех, у кого величина f(i) меньше. Таким образом мы приходим к решению: сразу при чтении данных запомним для каждого клиента величину f(i), отсортируем всех клиентов по этой величине и будем обслуживать в порядке возрастания до тех пор, пока хватает памяти в фотоаппарате.
Время работы — O(n·log(n)).
203D - Удар по мячу
Эта задача имеет два разных решения.
Решение 1. Будем последовательно двигаться по траектории мяча до тех пор, пока не влетим в поверхность двери. Для этого будем считать от каждой точки следующую точку, где текущий луч пересекает какое-либо препятствие (стена, дверь и так далее). Каждая точка на луче имеет вид (x + t·vx, y + t·vy, z + t·vz), где t > 0 — параметр. Подставим уравнения всех препятствий в этот вид и найдем минимальное t, а значит, и точку, где луч пересечет препятствие первый раз. Осталось только пересчитать vx, vy,vz и повторить процесс дальше до тех пор, пока мяч не влетит в дверь. Пересчитывать компоненты вектора скорости очень просто — при столкновении соотвествующую компоненту нужно просто умножить на - 1.
Время работы такого решения — O(X2), где X — максимальная из координат мяча в начальный момент времени.
Решение 2. Как известно, траекторию отражения луча света от зеркала можно считать прямой, если отразить относительно зеркала все остальные объекты. Для уточнения приведем рисунок: на нем можно построить траекторию движения луча от точки A к точке B отразив точку в B в B' и нарисовав отрезок AB’.

Аналогичную идею будем использовать в нашем решении. Каждую координату x или z будем находить независимо, рассмотрим для x, для z аналогично.
Допустим у нас нет стен, тогда мяч прилетел бы в точку с координатой 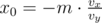 . Теперь допустим x0 > 0, а стена представляет собой прямую x = a. Тогда мысленно отразим наш коридор (то есть полосу между прямыми x = 0 и x = a) несколько раз, то есть получим множество прямых x = ka, где пространство между соседними прямыми — это одно из отражений коридора.
. Теперь допустим x0 > 0, а стена представляет собой прямую x = a. Тогда мысленно отразим наш коридор (то есть полосу между прямыми x = 0 и x = a) несколько раз, то есть получим множество прямых x = ka, где пространство между соседними прямыми — это одно из отражений коридора.
Посмотрим, сколько раз отрезок между точками (a / 2, m) и (x0, 0) пересекал прямые, и в зависимости от четности можно понять, от какой стороны коридора последний раз отразился мяч, прежде чем попал в дверь. А сам ответ несложно найти отложив величину x0 (mod a) (где "mod" означает остаток от деления нацело) от соответствующей стены.
Таким образом, описанное решение позволяет найти ответ за O(1).
203E - Перевозки
В этой задаче требуется рассмотреть два случая.
Первый — пусть все роботы едут самостоятельно. Тогда выделим множество роботов, у которых li ≥ d, отсортируем их по возрастанию количества требуемого горючего, и будем брать в этом порядке и отправлять в багажное отделение пока не кончится топливо. Этот случай похож на решение задачи C этого же раунда.
Второй случай рассматривает тех роботов, которые вкладывают друг в друга. Выделим множество роботов, у которых ci > 0, пусть из всего k штук, и пусть 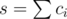 . Тогда несложно понять, что если мы всех этих роботов упакуем так, чтобы лишь
. Тогда несложно понять, что если мы всех этих роботов упакуем так, чтобы лишь 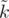 из них ехало самостоятельно, а остальные были вложены в другие роботы, то еще у нас останется
из них ехало самостоятельно, а остальные были вложены в другие роботы, то еще у нас останется 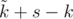 свободных слотов для других роботов.
свободных слотов для других роботов.
Таким образом, выделим множество роботов у которых ci > 0, li ≥ d — то есть эти те роботы, которые могут везти других роботов и при этом могут самостоятельно добраться до багажного отделения.
Переберем, сколько из таких роботов на самом деле поедут своим ходом (не забываем про ограничения на топливо), и по формуле выше найдем количество свободных слотов. Заметим, что мы уже в любом случае отправили всех роботов, у которых ci > 0, а значит остались только те, у которых ci = 0, пусть таких всего num.
Каждый робот может иметь 3 состояния: он займет один из слотов, он поедет своим ходом, если у него li ≥ d и если хватит топлива, или он вообще не поедет.
Известно, сколько имеется слотов, а значит можно найти, сколько роботов или поедут своим ходом, или останутся, а точнее их 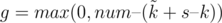 . Таким образом, нам надо найти среди всех роботов с ci = 0 и li ≥ d максимальное количество роботов (но не более, чем g штук), на которых осталось достаточно топлива. Остальные роботы поедут на свободных слотах или останутся (их известное количество).
. Таким образом, нам надо найти среди всех роботов с ci = 0 и li ≥ d максимальное количество роботов (но не более, чем g штук), на которых осталось достаточно топлива. Остальные роботы поедут на свободных слотах или останутся (их известное количество).
Эта подзадача решается предподсчетом величины f(i), означающую минимальное количество топлива, необходимое чтобы отправить i роботов среди тех, для которых выполняется ci = 0 и li ≥ d. По этой функции, очевидно, можно делать бинарный поиск.
Таким образом, соберем элементы решения: сначала переберем количество роботов, которые поедут своим ходом среди тех, у которых ci > 0, а затем с помощью бинарного поиска по предподсчитанной величине найдем, сколько роботов из оставшихся уместятся на свободные слоты, сколько поедут также своим ходом, а сколько останутся.
Не забудем про случай, когда вообще все роботы едут самостоятельно.
Мы получаем алгоритм, который можно реализовать за время O(n·log(n)).










