// Finally translated!
Hi everyone!
Do you like ad hoc problems? I do hate them! That's why I decided to make a list of ideas and tricks which can be useful in mane cases. Enjoy and add more if I missed something. :)
1. Merging many sets in 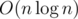 amortized. If you have some sets and you often need to merge some of theme, you can do it in naive way but in such manner that you always move elements from the smaller one to the larger. Thus every element will be moved only
amortized. If you have some sets and you often need to merge some of theme, you can do it in naive way but in such manner that you always move elements from the smaller one to the larger. Thus every element will be moved only 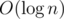 times since its new set always will be at least twice as large as the old one. Some versions of DSU are based on this trick. Also you can use this trick when you merge sets of vertices in subtrees while having dfs.
times since its new set always will be at least twice as large as the old one. Some versions of DSU are based on this trick. Also you can use this trick when you merge sets of vertices in subtrees while having dfs.
2. Tricks in statements, part 1. As you may know, authors can try to hide some special properties of input to make problem less obvious. Once I saw constraints like 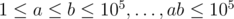 . Ha-ha, nice joke. It is actually
. Ha-ha, nice joke. It is actually 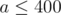 .
.
3. 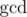 on subsegments. Assume you have set of numbers in which you add elements one by one and on each step calculate
on subsegments. Assume you have set of numbers in which you add elements one by one and on each step calculate 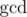 of all numbers from set. Then we will have no more than
of all numbers from set. Then we will have no more than 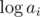 different values of gcd. Thus you can keep compressed info about all
different values of gcd. Thus you can keep compressed info about all 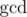 on subsegments of
on subsegments of 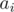 :
:
4. From static set to expandable via 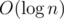 . Assume you have some static set and you can calculate some function
. Assume you have some static set and you can calculate some function 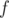 of the whole set such that
of the whole set such that 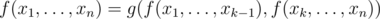 , where
, where 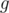 is some function which can be calculated fast. For example,
is some function which can be calculated fast. For example, 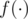 as the number of elements less than
as the number of elements less than 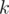 and
and 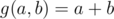 . Or
. Or 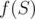 as the number of occurences of strings from
as the number of occurences of strings from 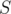 into
into 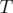 and
and 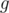 is a sum again.
is a sum again.
With additional  factor you can also insert elements into your set. For this let's keep
factor you can also insert elements into your set. For this let's keep  disjoint sets such that their union is the whole set. Let the size of
disjoint sets such that their union is the whole set. Let the size of 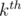 be either
be either  or
or 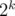 depending on binary presentation of the whole set size. Now when inserting element you should add it to
depending on binary presentation of the whole set size. Now when inserting element you should add it to 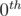 set and rebuild every set keeping said constraint. Thus
set and rebuild every set keeping said constraint. Thus 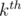 set will tale
set will tale 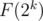 operations each
operations each 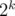 steps where
steps where 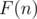 is the cost of building set over
is the cost of building set over 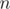 elements from scratch which is usually something about
elements from scratch which is usually something about 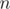 . I learned about this optimization from Burunduk1.
. I learned about this optimization from Burunduk1.
5.  -subsets. Assume you have set of numbers and you have to calculate something considering xors of its subsets. Then you can assume numbers to be vectors in
-subsets. Assume you have set of numbers and you have to calculate something considering xors of its subsets. Then you can assume numbers to be vectors in 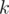 -dimensional space over field
-dimensional space over field 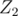 of residues modulo 2. This interpretation useful because ordinary methods of linear algebra work here. For example, here you can see how using gaussian elimination to keep basis in such space and answer queries of
of residues modulo 2. This interpretation useful because ordinary methods of linear algebra work here. For example, here you can see how using gaussian elimination to keep basis in such space and answer queries of 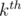 largest subset xor: link. (PrinceOfPersia's problem from Hunger Games)
largest subset xor: link. (PrinceOfPersia's problem from Hunger Games)
6. Cycles in graph as linear space. Assume every set of cycles in graph to be vector in 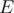 -dimensional space over
-dimensional space over 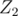 having one if corresponding edge is taken into set or zero otherwise. One can consider combination of such sets of cycles as sum of vectors in such space. Then you can see that basis of such space will be included in the set of cycles which you can get by adding to the tree of depth first search exactly one edge. You can consider combination of cycles as the one whole cycle which goes through 1-edges odd number of times and even number of times through 0-edges. Thus you can represent any cycle as combination of simple cycles and any path as combination as one simple path and set of simple cycles. It could be useful if we consider pathes in such a way that going through some edge twice annihilates its contribution into some final value. Example of the problem: 724G - Xor-matic Number of the Graph. Another example: find path from vertex
having one if corresponding edge is taken into set or zero otherwise. One can consider combination of such sets of cycles as sum of vectors in such space. Then you can see that basis of such space will be included in the set of cycles which you can get by adding to the tree of depth first search exactly one edge. You can consider combination of cycles as the one whole cycle which goes through 1-edges odd number of times and even number of times through 0-edges. Thus you can represent any cycle as combination of simple cycles and any path as combination as one simple path and set of simple cycles. It could be useful if we consider pathes in such a way that going through some edge twice annihilates its contribution into some final value. Example of the problem: 724G - Xor-matic Number of the Graph. Another example: find path from vertex  to
to  with minimum xor-sum.
with minimum xor-sum.
7. Mo's algorithm. Variant of sqrt-decomposition. Basic idea is that if you can do non-amortized insert of element in the set (i.e. having opportunity to revert it), then you can split array in sqrt blocks and consider queries such that their left ends lie in the same block. Then for each block you can add elements from its end to the end of the array. If you found some right end of query in that block you can add elements from the end of block to left end of query, answer the query since all elements are in the set and revert those changes then.
8. Dinic's algorithm in 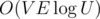 . This algorithm in
. This algorithm in 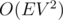 is very fast on the majority of testcases. But you can makes its asymptotic better by very few new lines of code. For this you should add scaling idea to your algorithm, i.e. you can iterate powers of 2 from k to 0 and while it is possible to consider only edges having capacity at least
is very fast on the majority of testcases. But you can makes its asymptotic better by very few new lines of code. For this you should add scaling idea to your algorithm, i.e. you can iterate powers of 2 from k to 0 and while it is possible to consider only edges having capacity at least 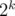 . This optimization gives you
. This optimization gives you 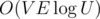 complexity.
complexity.
9. From expandable set to dynamic via  . Assume for some set we can make non-amortized insert and calculate some queries. Then with additional
. Assume for some set we can make non-amortized insert and calculate some queries. Then with additional  factor we can handle erase queries. Let's for each element x find the moment when it's erased from set. Thus for each element we will wind segment of time
factor we can handle erase queries. Let's for each element x find the moment when it's erased from set. Thus for each element we will wind segment of time 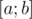 such that element is present in the set during this whole segment. Now we can come up with recursive procedure which handles
such that element is present in the set during this whole segment. Now we can come up with recursive procedure which handles 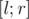 time segment considering that all elements such that
time segment considering that all elements such that 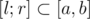 are already included into the set. Now, keeping this invariant we recursively go into
are already included into the set. Now, keeping this invariant we recursively go into 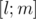 and
and 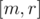 subsegments. Finally when we come into segment of length 1 we can handle the query having static set. I learned this idea from Burunduk1, and there is a separate entry about it (on dynamic connectivity).
subsegments. Finally when we come into segment of length 1 we can handle the query having static set. I learned this idea from Burunduk1, and there is a separate entry about it (on dynamic connectivity).
10. Linear combinations and matrices. Often, especially in dynamic programming we have to calculate the value wich is itself linear combination of values from previous steps. Something like 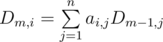 . In such cases we can write
. In such cases we can write 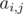 into the
into the 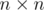 matrix and use binary exponentiation. Thus we get
matrix and use binary exponentiation. Thus we get 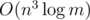 time instead of
time instead of 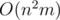 .
.
11. Matrix exponentiation optimization. Assume we have 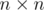 matrix A and we have to compute
matrix A and we have to compute 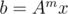 several times for different m. Naive solution would consume
several times for different m. Naive solution would consume 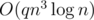 time. But we can precalculate binary powers of A and use
time. But we can precalculate binary powers of A and use  multiplications of matrix and vector instead of matrix and matrix. Then the solution will be
multiplications of matrix and vector instead of matrix and matrix. Then the solution will be 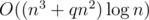 , which may be significant. I saw this idea in one of AlexanderBolshakov's comments.
, which may be significant. I saw this idea in one of AlexanderBolshakov's comments.
12. Euler tour magic. Consider following problem: you have a tree and there are lots of queries of kind add number on subtree of some vertex or calculate sum on the path between some vertices. HLD? Damn, no! Let's consider two euler tours: in first we write the vertex when we enter it, in second we write it when we exit from it. We can see that difference between prefixes including subtree of v from first and second tours will exactly form vertices from v to the root. Thus problem is reduced to adding number on segment and calculating sum on prefixes. Kostroma told me about this idea. Woth mentioning that there are alternative approach which is to keep in each vertex linear function from its height and update such function in all v's children, but it is hard to make this approach more general.
13. Tricks in statements, part 2. If k sets are given you should note that the amount of different set sizes is 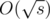 where s is total size of those sets. There is even stronger statement: no more than
where s is total size of those sets. There is even stronger statement: no more than 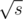 sets have size greater than
sets have size greater than 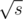 . Obvious example is when we are given several strings with total length s. Less obvious example: in cycle presentation of permutation there are at most
. Obvious example is when we are given several strings with total length s. Less obvious example: in cycle presentation of permutation there are at most  distinct lengthes of cycles. This idea also can be used in some number theory problems. For example we want calculat
distinct lengthes of cycles. This idea also can be used in some number theory problems. For example we want calculat 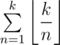 . Consider two groups: numbers less than
. Consider two groups: numbers less than 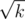 we can bruteforce and for others we can bruteforce the result of
we can bruteforce and for others we can bruteforce the result of  And calculate how many numbers will have such result of division.
And calculate how many numbers will have such result of division.
Another interesting application is that in Aho-Corasick algorithm we can consider pathes to the root in suffix link tree using only terminal vertices and every such path will have at most 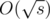 vertices.
vertices.
14. Convex hull trick. Assume we have dp of kind 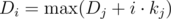 , then we can maintain convex hull of linear functions which we have here and find the maximum with ternary search.
, then we can maintain convex hull of linear functions which we have here and find the maximum with ternary search.
15. xor-, and-, or-convolutions. Consider ring of polynomials in which 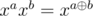 or
or 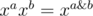 or
or 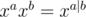 . Just like in usual case
. Just like in usual case 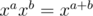 we can multiply such polynomials of size
we can multiply such polynomials of size 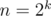 in
in 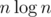 . Let's interpret it as polynomial from
. Let's interpret it as polynomial from 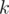 variables such that each variable has power ≤ 1 and the set of variables with quotient
variables such that each variable has power ≤ 1 and the set of variables with quotient 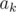 is determined by binary presentation of
is determined by binary presentation of 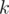 . For example, instead of
. For example, instead of 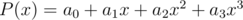 we will consider the polynomial
we will consider the polynomial 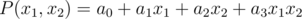 . Now note that if we consider values of this polynomial in the vertices of cube
. Now note that if we consider values of this polynomial in the vertices of cube 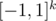 then due to
then due to 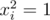 , we can see that product of such polynomials will use exactly xor rule in powers. or-convolution can be done in the same way considering vertices of
, we can see that product of such polynomials will use exactly xor rule in powers. or-convolution can be done in the same way considering vertices of 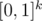 and having
and having 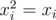 . and-convolution you can find yourself as an excercise.
. and-convolution you can find yourself as an excercise.
Finally I may note that or-convolution is exactly sum over all submasks and that inverse transform for xor-convolution is the same with initial one, except for we have to divide everything by n in the end. Thanks to Endagorion for explaining me such interpretation of Walsh-Hadamard transform.
16. FFT for two polynomials simultaneously. Let 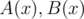 be the polynomials with real quotients. Consider
be the polynomials with real quotients. Consider 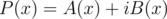 . Note that
. Note that 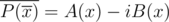 , thus
, thus 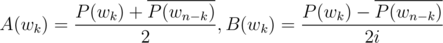 .
.
Now backwards. Assume we know values of 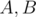 and know they have real quotients. Calculate inverse FFT for
and know they have real quotients. Calculate inverse FFT for 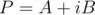 . Quotients for A will be real part and quotients for B will be imaginary part.
. Quotients for A will be real part and quotients for B will be imaginary part.
17. Modulo product of two polynomials with real-valued FFT. If mod is huge we can lack accuracy. To avoid this consider 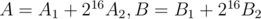 and calculate
and calculate 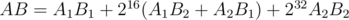 . Using the previous point it can be done in total of two forward and two backward FFT.
. Using the previous point it can be done in total of two forward and two backward FFT.










Nice list! Could you clarify the 4th trick? What do we exactly want to calculate, and how does the trick help us?
For example, if f denotes the number of elements less than k and g(a, b) = a + b, does this mean that we want to calculate the number of elements less than k in the set? Why can't we just have a counter and increase its value by one if the new element is less than k?
It's solving "decomposable searching problems". I first saw the trick here.
Thanks! So apparently k is not a constant here.
For point 12 (Euler tour magic)
"We can see that difference between prefixes including subtree of v from first and second tours will exactly form vertices from v to the root"
I'm not really sure what this means. I know a subtree of v is a contiguous range in first tour but not sure what it means for the second tour.
It means the same for the second tour.
Just in the first way every time we "open" (enter) some subtree we write its root index down. In the second way we're writing down the moments when we "close" a subtree (left it/completely processed it).
So if you're looking at the prefix that contains some subtree of
uin both Euler's tours the difference between 2 prefixes are vertices whose subtree has been opened but not yet closed. And these vertices are parents ofu(= lie on the path from root tou)In what context is Euler Tour being mentioned in Point 12?
Isn't Euler Tour by definition supposed to include every vertex each time we visit it?
Then what does this line mean?
Let's consider two euler tours: in first we write the vertex when we enter it, in second we write it when we exit from itThis may be common knowledge, but it was mind-blowing to me when I first discovered it:
Avoiding re-initialization: Especially in graph-traversal or DP problems, you may be calling a subroutine multiple times, needing to initialize an array each time:
In cases where this re-initialization is the bottleneck of your program, or if your implementation is just slightly too slow to pass in time, it can be improved by using a sentinel and avoiding re-initialization each time:
The only change would be that instead of checking
visited[i] == -1, you would checkvisited[i] != sentinel. I used this trick recently in a problem where a BFS subroutine was to be called in every query. Changing thevisitedarray from boolean to int and using this trick helped me squeeze my solution into the time limit. Hope it helps!This is an optimization, but only a constant one. You could keep track of invalidated indexes in a vector (those i for which visited[i] became true) and reinitialize only these indexes. But your way is more convenient, of course.
Point 10: It should be O(n2log(m)), right?
UPD: Got it, it was mentioned using naive multiplication (n3). I was thinking about Cayley Hamilton Method (n2).
Can you elaborate on the method? If you're talking about this, it only applies for linear recurrences..
Anybody can provide example problems for these methods?
Some problems for first idea here: http://codeforces.com/blog/entry/44351
What about a blog have segment tree tricks?
What is the advantage of fourth method? Why can't I just use set?
PS. thanks for this excellent post
If I understand it well enough, it seems to me like the 4th point is also achievable with implicit key treaps. Operations on them are logarithmic (average case), they allow you to insert elements on any position and they can answer any range queries as long as the answer for a query of a subset can be computed quickly from the answers of the query of two of its subsets, which seems to be what point 4 is trying to achieve.
For #16, how do we compute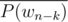 so that we can then compute
so that we can then compute 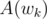 and
and 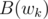 ?
?
I think we're supposed to compute the forward FFT of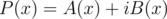 but I don't see how we get
but I don't see how we get 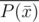 from that.
from that.
Sorry if this is simple, but I'm not able to see it.
Umgh, you know P(wn - k) so you just take conj(P(wn - k))
...Yep, it really was that simple. Thanks for your time.
Thanks a lot, man :). Really the tricks are so amazing, especially number 12. I have solved a problem using this trick. Problem link I will be grateful to u if u provide some problems that can be solved using trick 12. Thanks :)
prodipdatta7, Here you go.
Can anybody explain 3rd trick?
Decompose any number, say
n, into it's prime factors. Now when thegcdof the segment changes it must decrease by atleast half (Why? That's the least prime factor you can have). So there are atmostlog(A[i])+1different values.Can you explain it through an example please? Thanks for reply:)
How to prove statement in trick 13 "no more than
sqrt(n)sets have size greater thansqrt(n)" ?I am assuming $$$n$$$ is the sum of the sizes of all sets.
Suppose there are more the $$$\sqrt{n}$$$ sets with size greater the $$$\sqrt{n}$$$. Let $$$x$$$ be the sum of these sets, then $$$x > \sqrt{n} * \sqrt{n} = n$$$ which is a contradiction, because $$$x$$$ can not be greater than $$$n$$$.
#6 is called the cycle space. More details are in the Wikipedia article: https://en.wikipedia.org/wiki/Cycle_space
I am unable to understand Trick 1. Can anyone provide a better reference to understand Trick 1?
I doubt a grey guy could understand it anyway.
Well, I am here to clear your doubt that I understood it. Maybe I am slow but I do understand.
You should make a blog about it so others can understand.