If you are registered on Timus, then you should have been received e-mail with invitation to this contest. The contest will be on 19 November in 11 Moscow time.
It was a junior championship but it was 'a little' harder than it was intended. As I remember, Merkurev solved all the problems with only 15 minutes to go, so I think that this contest may be interesting for participants with different levels, up to the strongest ACM teams.
The duration is 5 hours, standard ACM rules. It is a team (up to 3 participants) contest but you are welcome to partcipate individually too.
The authors of the problemset are Um_nik, sivukhin, kb., Tinsane and crassirostris.
Auto comment: topic has been translated by Um_nik (original revision, translated revision, compare)
What is the idea behind problem K?
Can anyone tell me how to solve I?
I solved using bitset: solution
Full editorial in Russian
Short solution ideas:
A (author Um_nik) — just do what is written in statement
B (Um_nik) — One of the rectangle sides will be on one of triangle sides. If we'll fix that triangle side there will be no more than 2 rectangles. We can find them explicitly. Don't forget about traingles with big angle (>= 90 degrees). Solution can be written in rational numbers in Java/Python but double solution is also OK.
C (Tinsane) — iterate prime numbers, if the number of prime numbers our number have is small and current prime is big then the answer is NO.
D (Um_nik) — it is easy to construct path with length no more than 3. For shorter path write bruteforce starting from T (each number have small number of divisors, it will be fast).
E (sivukhin) — write stupid retrograde analysis, it will work in
time. Can be optimised to O(n) using sime prefix sums.
F (sivukhin) — Let the sum of distances traversed by Alice and Bob be L. Then the answer is S / L
G (crassirostris) — just do what is written in statement. May look terrifying, but my solution in Python is easy 40 lines of code (and I'm not a master of Python). Be careful with integer (and even long long) overflow.
H (Um_nik) — every such function must be a permutation. Permutation can be decomposed to some cycles. We want all cycle lengths in our permutation be a divisor of k. Initially we have some cycles and chains, we can join chains and make cycles from chains. We can write an O(3n) DP on subsets but it will be too slow. Notice that chains of length 1 are special — it will lead to O(3n / 2) and even O(2n / 2n2) solutions. Also it can be solved with some smart bruteforces, one of them actually works for n up to 55.
I (kb.) — just do n iterations trying all the rules. Complexity will be O(n2m) which is not fast enough. But we can speed it up using bitsets. Also we can store a pointer to first missing pony in every rule, thus obtaining O(nm) solution.
J (Tinsane) — standard problem with some queries on segments. Let's find LCA (of two vertices) using sparse table, and the build another sparse table to answer queires. Complexity will be
, but constant factor is quite large. I_love_Tanya_Romanova got AC with O(log2n) per query solution.
K (Um_nik) — if we can save at least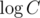
elements then we can get OR of all array, which is obviously maximal. So if 
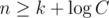then the problem is trivial. Now we'll solve two problems separately: bruteforce for small k and knapsack-like DP for small C.
Thanks for the contest :)
For problem H, how do you get O(2n / 2n2) ? I saw the 3n / 2 but I thought it might be too slow, so I went to sleep instead :P
DP state: dp[mask][curChainLen]
For problem D, what's the answer for 5 1000000007 Is 2 4 5 4 1000000008 1000000007 minimal?