→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/24/2024 23:30:22 (j2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Is it just me or are this year's COCI rounds significantly harder than the last year's?
Yeah you are absolutely right.
Can someone please share their approach for problem C?
I used bitmask DP, each bit representing whether a bottle still has water or not. It runs in O((n2)(2n)).
Thanks!
Yep, and at a given state you have to iterate trough all the pairs and try to pour water from a glass with water to the other glass with water
Yeah, that's exactly what I did. Just realized I typed a variable name incorrectly and got 0!!! T0T
can you share your code pls
Here is my solution for problem C.
Same, but I doubt it's fast enough when n=20
It is fast enough; I tested with max case and it ran amazingly in like 0.05s. The server is just really fast.
i submitted a dp bitmask O(n^2 2^n), the max runtime is 1,91 s
could you tell me how to optimize the code?
https://ideone.com/klSTpa
Sorry, just realized it worked fast because my solution skipped a lot of iterations (it was incorrect, but the correct version works in 0.85s). Maybe your solution is slower because of recursion. Bottom-up should work faster.
Here's my code.
you can also use some bitwise tricks to optimize
my code runs at most 0.51s on the server in Test#9
You can also achieve O(N * 2N) if you precompute for each set bit of a mask his optimal pair (where you should pour the water to). The downside of this solution is the O(N * 2N) memory complexity, which doesn't fit in the ML that easily. For each mask we are only interested in the set bits, so a part of the table will never be used. We will need only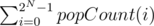 cells. Here is my sketch of this idea, however i didn't manage to fit the last 2 tests into ML.. maybe someone else will. The next idea which comes in mind is to only use the stricly needed number of bits for each table, with packed bit fields.
cells. Here is my sketch of this idea, however i didn't manage to fit the last 2 tests into ML.. maybe someone else will. The next idea which comes in mind is to only use the stricly needed number of bits for each table, with packed bit fields.
My solution has O(N * 2N) time complexity and O(2N) space complexity.
I used a greedy approach like Kruskal's Algorithm for Minimum Spanning Tree.
The difference is that I stop connecting vertices when there are K connected components left.
I'm not sure whether my solution is correct or not.
UPD: I'm wrong, just ignore me QAQ
Maybe you didn't notice that cij doesn't necessarily equal cji...
The writer of the announcement
The polygon is simple, but it's not necessarily convex so there is no point in providing points in some sort of ccw order.has no idea what he is talking about. In most of geometry tasks it is really useful to know if the vertex order is counterclockwise or clockwise. Also in this task I had to make sure that the vertices are in counterclockwise order by computing the signed area.Yes, you are right, the writer of the announcement made a mistake. Although, it isn't very difficult to check whether the points are given in ccw order.
But, again, I agree with you and would like to apologize for that in the name of the organizers.
Anyone know when results are generally released?
Actually, it is ~1.5 hours, but sometimes, it could be half an hour or even tommorow.
Results are out!
Can someone please share their approach for problem E?
The problem can be reformulated as: Label the numbers in
[2..N]with either 0 or 1. The final array will be: the numbers labeled with 0 in reverse order, followed by the first number followed by the numbers labeled with 1 in the initial order. Now you need to count for every such configuration of 0 and 1 what is the number of maximum increasing subsequences. If you traverse the array from finish to start, then from start to finish in this order and maintain the classic Fenwick tree for keeping and counting maximum increasing subsequences, in the end you will have counted the number of ways to form a maximum increasing subsequence and label the numbers in your subsequence with 0 or 1. You don't need to worry about using a number twice(the subsequence is strictly increasing). Now you need to multiply this by the number of ways to label the elements that you didn't use in the subsequence. It will be2^(N-M)if you have used the first element in your subsequence and2^(N-M-1)otherwise, where M is the size the maximally increasing subsequence. So you should solve for these two cases separately.For each position we can calculate the longest increasing subsequence (LIS) ending with that position, and the number of ways to achieve that maximum. We calculate the same thing for the longest decreasing subsequence (LDS) starting from a position.
Now, it can be seen that the solution is a union of an increasing and a decreasing subsequence such that the smallest number in the LIS is greater than the greatest number in the LDS. All the moves that don't involve those positions can be arbitrary. Also, in some implementations, it is necessary to treat the first position a bit differently, but those are just details.
The test 16d in Meksikanac has k = 66332 even though in both English and Croatian statements and in the messages it says that k ≤ 10000. Most of other tests in groups 11-16 have the same problem.
We are currently fixing the issue.
Hi,
I made a mistake when generating test data for this task and would like to apologize. We are currently investigating to what extent did this influence other contestants and will swiflty decide on how to proceed. From what we have seen thus far, it is very likely that you had the only submission where this makes any difference and we know your code gets accepted even with the larger constraint.
Again, I'm really sorry for the inconvenience.
For problem B I tested locally the test cases my program received SIGABRT and it works fine, however in the Test section of the contest it shows bad_alloc error.
My code: Clcik
Is java.awt never allowed? I tried using it in-contest but I was given a compile error after submission that said "package java.awt does not exist". Just wanted to make sure this was intentional since I'm fairly certain java.awt should work with javac 1.8.0_102 and I didn't see anything saying that it was not allowed.
how to solve problem D?
First observation: Suppose for some expression A we can obtain the maximum value C (considering the boundary Z), then we can choose the value for this expression any number in [0, C].
For expression B which has some inserted expressions A1, A2, ..., Ak, we, therefore, obtain the array C1, C2, ..., Ck which is the maximum values of these expressions: We have 2 cases:
Sum
It is quite trivial so if we can choose for expression with index i any number in [0, Ci], then for the sum of these expressiosn we can choose any value in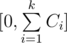 , and the answer is
, and the answer is 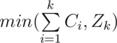
Product
It is somehow tricky, and I don't know how to prove it, but I will try to explain:
The best case for the product of k terms whose sum is S is when all terms are equal to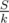 . So the best strategy is to equalize terms. My approach was sorting the array C and trying to make them equal by making each term equal to
. So the best strategy is to equalize terms. My approach was sorting the array C and trying to make them equal by making each term equal to 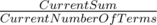 , so if I can't make some element the optimal value, I will try to equalize the remaining ones.
, so if I can't make some element the optimal value, I will try to equalize the remaining ones.
My code.
P.S. Would be grateful for someone posting the proof of product case for this problem
P.P.S. Sorry for such incomplete explanation
Is AM–GM inequality what you need to prove it?
How to solve B efficiently?
I have used 2d dp, going from (1, 1) to (N, M) in each position I've been choosing better alternative. Bottleneck of this approach is that string comparisons required at each step, so I was expecting to get TL and I got it. But I am still thinking how to solve this better.
Any ideas / hints ?
just bfs from (1, 1) to (N, M)
you only have to consider the states that are currently lexicographical smallest, so their prefix are the same
therefore, you don't have to store the entire string for each state
their coordinates are enough
Couldn't take part since it clashed with codechef's lunchtime :(