Suppose we want to solve a problem by doing binary search on answer. Then the answer will be checked against jury's answer by absolute or relative error (one of them should be smaller then ε). For simplicity we will assume that our answer is always greater than 1 and smaller than B. Because of that, we will always use relative error rather than absolute.
Suppose we have made n iterations of our binary search — what information do we have now? I state that we know that real answer is lying in some segment [xi, xi + 1], where 1 = x0 < x1 < ... < xi < ... < x2n = B. And what is great — we can choose all xi except for x0 and x2n.
Now, for simplicity, we will also assume that we will answer xi + 1 for segment [xi, xi + 1] and the real answer was xi — it is the worst case for us. It is obvious that we will not do that in real life, any other answer would be better, but you will get the idea.
So, what is our relative error? It is 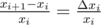 . Worst case for us is when relative error is maximal. It is logical to make them equal — exactly what we do by binary search with absolute errors.
. Worst case for us is when relative error is maximal. It is logical to make them equal — exactly what we do by binary search with absolute errors.  . We can assume that
. We can assume that 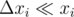 so
so 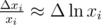 . Now we have
. Now we have 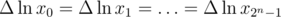 , but
, but  , so
, so 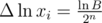 . How large should be n to get error less than ε?
. How large should be n to get error less than ε? 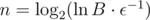 . Much smaller than
. Much smaller than 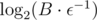 .
.
How to write such binary search? We want to choose m in such a way that 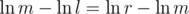 or simply
or simply 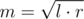 .
.
Now I want to deal with some assumptions I made.
How to choose answer in the end? Again, 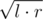 (it is basically the same as dividing the segment in binary search).
(it is basically the same as dividing the segment in binary search).
What to do if the answer can be smaller than 1? Try 1; if answer is smaller than 1~--- use standard binary search (because absolute error smaller than relative); is answer is bigger than 1~--- use the binary search above.
P.S. I have never heard about this idea and come up with this while solving 744D - Hongcow Draws a Circle. I'm sorry if it is known for everyone except for me.











Even if this idea is known by all top tier competitive programmers, it's always good for the ones that are learning to read something like this.
Nice analysis! Thanks
I think these should be attached as special editorials for the problems,so that noobs like me get it easily in what direction to go!!
Let's do less iterations, but replace (l + r) / 2 (what is float sum and decrementing exponent) to sqrt(l * r) (what is float multiplication and taking square root)?
Wow, such a cool optimization.
Often iteration takes a lot (e.g iteration over long array) so 1 square root per operation may be negligible
I'm pretty sure he understands it.
If you think everybody oughta know everything you know, congrats, you're typical snob.
Is it true for small segments?
I don't really feel good about this step. The xi are discrete so Δ is just a difference operator (Δ xi = xi + 1 - xi), where as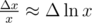 comes from differentiating the continuous integral for
comes from differentiating the continuous integral for 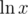 . This seems like abuse of notation to me. The whole point of this proof is to determine the correct way of picking the xi, using information about them that don't follow from any assumptions seems wrong.
. This seems like abuse of notation to me. The whole point of this proof is to determine the correct way of picking the xi, using information about them that don't follow from any assumptions seems wrong.
Maybe I'm oversimplifying things, but the idea is basically to find a formula for the midpoint which minimizes the worst case relative error you might get. As you already said, if you end up with interval [l, r], the worst you can do is guess r when the answer is l, i.e. the worst possible relative error is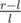 . In other words, we want to find the m that minimizes:
. In other words, we want to find the m that minimizes:
(Since we don't know if we continue with the left interval or with the right interval, we take the maximum of the worst case relative errors of either interval.)
It's pretty clear that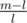 is increasing in m (it's a linear function) and that
is increasing in m (it's a linear function) and that 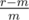 is a decreasing function in m (rewrite as
is a decreasing function in m (rewrite as 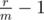 ), so their maximum is minimal when they are equal, i.e. we have to solve
), so their maximum is minimal when they are equal, i.e. we have to solve  . Multiply by ml and subtract ml from both sides, and you end up with m2 = lr, and since we required that l ≤ m ≤ r, only
. Multiply by ml and subtract ml from both sides, and you end up with m2 = lr, and since we required that l ≤ m ≤ r, only 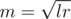 is a valid solution (when we assume, as in the blogpost, that l, r > 1.
is a valid solution (when we assume, as in the blogpost, that l, r > 1.
So clearly following the rule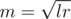 optimally minimizes the relative error after a single iteration, but of course the question is, does this hold after multiple iterations? (or is this an incorrect greedy solution) So, more generally, in the n-th step of the binary search we want:
optimally minimizes the relative error after a single iteration, but of course the question is, does this hold after multiple iterations? (or is this an incorrect greedy solution) So, more generally, in the n-th step of the binary search we want:
(where l functions as x0 and r as x2n)
If you only vary xi then by logic similar to the above we trivially find that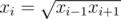 . It's pretty easy to work out that
. It's pretty easy to work out that 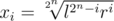 is a solution to this system (this is a direct formula for xi that you get by repeatedly applying the
is a solution to this system (this is a direct formula for xi that you get by repeatedly applying the 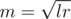 rule). However, I'm not really sure how to prove that this is the optimal (and only?) solution. Can a more competent mathematician finish the proof?
rule). However, I'm not really sure how to prove that this is the optimal (and only?) solution. Can a more competent mathematician finish the proof?
(pointing out that we have 2n - 1 equations and 2n - 1 unknowns (we already know x0 and x2n: l and r) probably doesn't apply for these kinds of systems?)
I don't think it's abuse of notation. wiki
Let's prove that
by induction on $p$ and q.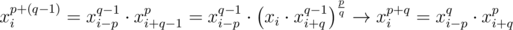
Add 1 to each term. Their product becomes r/l, which is a constant, so the geometric mean is trivially optimal.
The real issue here (and it keeps coming up over and over in many contexts) is that optimizing with the form (delta X)/X intrinsically breaks some symmetries based on your chosen basis; while simple binary search doesn't.
The final numeric answer if resolvable will be identical, but if you're computing approximations with floating point accuracy, you might get another terminator lock down :)
I feel like I have something to contribute here. If our outputted answer is $$$x$$$ and the Jury's answer is $$$y$$$, then the score we get is $$$|1-\frac{x}{y}|$$$. Notice that $$$\ln(\frac{x}{y}) is just \ln(x) - \ln(y)$$$. Since $$$\ln(\frac{x}{y})$$$ increases as $$$\frac{x}{y}$$$ increases. Trying to make $$$\ln(\frac{x}{y})$$$ as close to $$$0$$$ is the same as trying to make $$$\frac{x}{y}$$$ as close to $$$1$$$ as possible. Then, if we take the natural log of both of our endpoints, we are trying to find the value of $$$\ln(x)$$$ in the range $$$[0, \ln(B)]$$$ which is as close to the value of $$$\ln(y)$$$ as possible, which we can clearly do by a standard binary search, and which gives the complexity described above.