I have recently encountered this problem:
"Given an array a1, a2, ..., an, (1 ≤ n ≤ 105, 1 ≤ ai ≤ 106), count the number of subsequence ap1, ap2, ..., apk that ap1&ap2&...&apk = 0 (print the remain of division of that number by 109 + 7"
The best solution that I can come up is a dynamic programming solution that is not fast enough to solve this problem. How to solve this problem?
Thanks in advance.










Auto comment: topic has been updated by xuanquang1999 (previous revision, new revision, compare).
I'm not sure about this soultion.
Let's count all subsequences — 2^n. Now let count all subsequences with their and greater than 0. For all masks save count of numbers, that the mask is their submask. So using inclusion-exclusion principle we can calculate the answer.
UPD: OK
Ignore.
Here is the same task on codeforces : 449D - Jzzhu and Numbers. Maybe it will be helpful.
We were doing it on extra classes before a few days, but I do not know part with calculating function f from editorial.
This blog will surely help. SOS DP.
It can also be solved using this FFT-like transform (see transform for AND). My AC: 22102892 (though it required an optimization because it is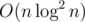 )
)
That was wrong, ignore it
Isn't this solution for substring not subsequence?
Yes, you are right.