Good day! Here, I wrote another of problem "С" from CBR #1
First find the radius of the circle of our triangle, this is the radius of the desired n-gon. Denote the radius of the circle through R. Then R = abc / 4S, where a, b, c - sides of the triangl, S - area of a triangle. We find all the angles of this triangle and denote them as A, B, C. The angles A, B, C can be found on this formula:
A = acos((b2 + c2 - a2) / (2bc))), B, C computes similarly. Now we find n.It here so: n = pi / gcd(A, B, C). Now we know R and n, with which we can find the area n-gon by this formula: n / 2 * R2 * sin(2pi / n).
Note that gcd (A, B, C) = gcd (gcd (A, B), C)
and the function gcd (x, y) can be calculated as follows:
double gcd(double x, double y) {
while (fabs(x) > eps && fabs(y) > eps) {
if (x > y)
x -= floor(x / y) * y;
else
y -= floor(y / x) * x;
}
return x + y;
}
//eps = 1e-4











Need the explanation of formula 1. n = pi / gcd(A, B, C) and
2. n ploygon area = n / 2 * R2 * sin(2pi / n)
I couldn't understand The first formula but I understood the second one, The condition in the problem is somewhat like this.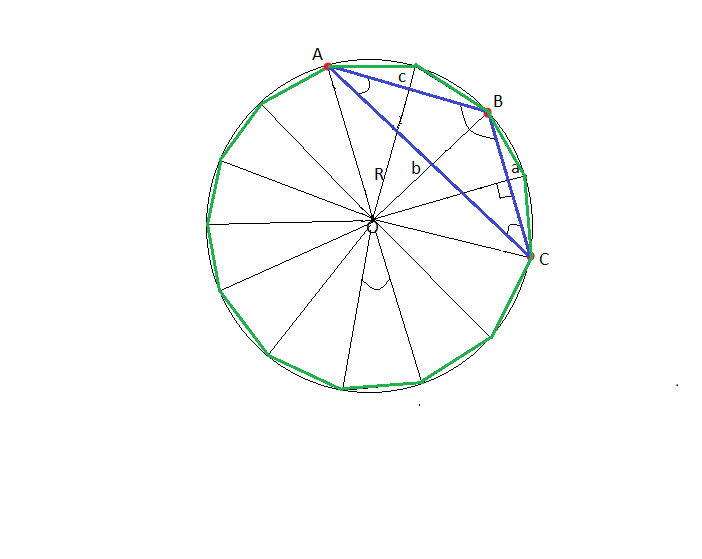 Here we can see that a n sided regular polygon is composed of n triangles all of which have a vertex at the center of the circle. So to find the total area we select one of the triangle's like this and find it's area and multiply it by n.
Here we can see that a n sided regular polygon is composed of n triangles all of which have a vertex at the center of the circle. So to find the total area we select one of the triangle's like this and find it's area and multiply it by n.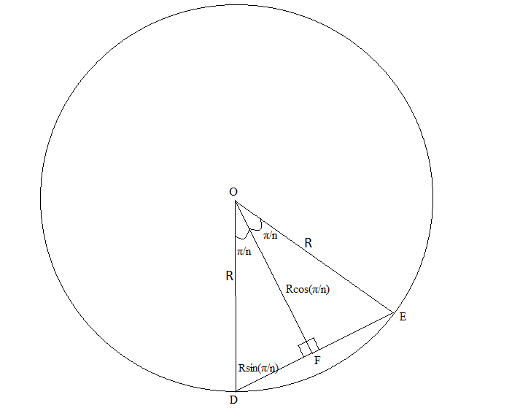 We know the central angle of each such triangle is
We know the central angle of each such triangle is 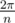 and from the figure we see that OF = (R cos (
and from the figure we see that OF = (R cos ( ))
)) )) also DE = 2Rsin (
)) also DE = 2Rsin ( )
)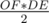 ) =
) =  (R cos (
(R cos ( )) (2Rsin (
)) (2Rsin ( )) = (
)) = (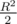 ) sin (
) sin (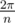 )
) ) sin (
) sin (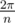 )
)
and DF = (R sin (
So Area of ODE is (
Total area = (
The images were made with MS Paint so I apologize for the quality. I followed whatever the editorial said and got AC 9274841.
.
You should not judge one who made a mistake ( to your mind ) almost 2 years ago. Use time machine !
How do you prove that N = PI / (gcd(A, B, C)) ?
2 * Pi / Nis an angle from the center of the сircumscribed circle between two closest vertices of desired polygon. Then angles from the center between two vertices of triangle will bea * (2 * PI / N),b * (2 * PI / N)andc * (2 * PI / N), wherea + b + c = N. Now let's notice, that the angles of our triangle (A, B, C) are inscribed angles of the сircumscribed circle. ThereforeA = a * (PI / N), etc. Thereforegcd(A, B, C) = PI / N. It is also true ifgcd(a, b, c) > 1, because it is beneficial to take the least N.can someone help me with the concept of epsilon in finding the gcd. Why do most of the accepted answers have it as 10^-4 . when i reduce it to 10^-5 , i get incorrect answer. Can someone tell me how did we decide this value because i think that lesser the value of eps meant a more precise answer??