A king wishes to go for a walk of a square chessboard with the following conditions: • Each two consequent cells of the path must be adjacent, i.e., share an edge or a corner (thus, a cell may have up to eight adjacent cells). • Each cell must be visited exactly once; the first and the last cells of the path must coincide (thus, the first cell of the path will be actually visited twice). • The path must have no self intersections (we may think of a path as a closed polyline with vertices at cells’ centers). Your task is to find the maximal possible length of a king’s path (here we mean the length of the polyline, not the number of king’s moves).
Sample Input
N=1 ans=0 N=2 ans=4 N=3 ans=9.414
I am not able to get it , would you please help me understand to this ? Thank you .











I tried a kind of brute force with some pruning for smaller values of N and found a pattern. For a board of size N * N, all cells will be visited and out of the N2 steps the king makes, (N - 2)2 will be of length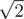 and the rest will be of length 1, so the answer is simply
and the rest will be of length 1, so the answer is simply 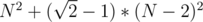 . I don't know how to prove it though.
. I don't know how to prove it though.
Thanks tenshi_kanade , but i was looking for proof .