The final round of the Finnish Olympiad in Informatics (Datatähti) will take place tomorrow, and after the official contest, there will be an international online contest.
The online contest will be available at CSES:
The length of the contest will be 5 hours, and there will be 5-7 tasks of varying difficulty. The contest will follow the IOI rules: full feedback and no penalty for multiple submissions. Available languages are C++, Java, Pascal and Python.
The online contest will be a virtual contest, which means that you can start the contest at any time between 19 Jan 2017, 18:00 and 22 Jan 2017, 18:00 (UTC).











The online contest has started!
Remember that today is the last chance to participate!
The results will be published immediately after the contest.
I'm currently participating, will we be able to upsolve once it finishes?
Yes
Where can we find the results?
Some people are still coding. I'll post a link to the results here when the contest is over.
Contest results
Congratulations to eduardische for winning the online contest by getting more than 19 points in the last task!
The best score in the official contest was 554 points by siiri.
Thanks! This was a really fun competition.
For the record, my 51 points solution to the last task is as follows. Take any function that can translate ID to dishes (I assumed simply taking modulo 3 would have counter-examples, so I took a random number from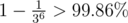 , you have 50000 queries overall (I haven't realized that for a while and just assumed my function was not random enough, creating quite hilarious random function complications throughout the contest). I'm really interested to hear the full solution to this problem.
, you have 50000 queries overall (I haven't realized that for a while and just assumed my function was not random enough, creating quite hilarious random function complications throughout the contest). I'm really interested to hear the full solution to this problem.
rand()after fixing the seed withsrand(ID)), Then with a high chance you're going to have small groups (consecutive table segments with same dish order) and you're going to see entirety of the group (including boundaries) in the data given. Give every odd person in the group his original order, but replace every even person's dish with the one that is not the dish of the next group on the right. That way no matter what the group size is, you avoid clashes within the group and with the neighboring groups. Unfortunately, you sometimes won't see even one side of the group in the final subtask because while the chance of seeing one boundary isThe key idea is to focus on "colour reduction".
Initially, the IDs give a proper colouring of each table with 1e9 colours. That is, each person is labelled with a number from [1e9], and adjacent people have distinct labels.
We will repeatedly apply a colour reduction operation: given a proper colouring with a large number of colours, produce a new proper colouring with a small number of colours. Furthermore, we will do it locally: everyone can pick their new colour f(x,y) if they know x = their own old colour and y = the old colour of their successor.
Note that f has to work so that if x ≠ y and y ≠ z, then f(x,y) ≠ f(y,z). That is, as long as the old colouring is proper, the new colouring is also guaranteed to be proper.
With a bit of thought, it is fairly easy to come up with such a function f that reduces the number of colours from 2^k to 2k; this is known as the Cole–Vishkin algorithm. So if you start with a colouring with at most 2^32 colours, one step reduces it to 64 colours, and another to 12 colours. Unfortunately, if we continue any further this way, we won't make progress fast enough.
But we can do better. It is possible to find a function g that reduces the number of colours from (2k choose k) to 2k; this is known as the Naor–Stockmeyer algorithm. With this algorithm we can reduce from 12 to 6 colours in one step, and from 6 to 4 in another step.
Four steps so far in total. We started with tables properly coloured with 1e9 colours, and we knew a sequence of 7 colours around you. Now we are left with tables properly coloured with 4 colours, and we know a sequence of 3 colours around you. Now it is easy to come up with an ad-hoc rule that gets you down to 3 colours.
I won't spoil all the fun of how to construct functions f and g, but the numbers 2^k and (2k choose k) are hints: try to interpret the original colour as a string of k bits, or as a subset of size k from a base set of size 2k.
I see, thanks a lot for the explanation!
Can someone tell me how to solve B without using a segment tree?
You can maintain a set of nonnegative values (up to 10^5) that are not in the current subarray. The smallest of them is the mex value of the subarray.
Thanks, that's a nice solution!
Solved it using map and some optimization,my approach was kind of naive.. Simply take the first subset 0 -> k,calculate the current mex in the map then 1 -> k+1,(you wont have to loop over the array anymore, just loop over the map to find the first positive integer that didn't appear) 2 -> k+2, And so on..
you will have to calculate the mex each time, but there are few times where the mex doesn't change
Lol, I was solving like this: A-F ez, done with pretty much no effort at all; G: FUG:DDDD, not even trying.
Also, I upgraded my template for this contest only.
I thought Finland is best known for things like sauna, Sibelius, etc., but it seems that the reality is very different :D
How to properly approach problem E (Grid) ? I mean, how did you start thinking and come to the solution ?
In my case, I wrote a exponential solution and tried to find a pattern. It was really tiresome and it took me way too much time. So I wonder how you guys did it.
My solution for larger N was: make a random solution; while some row/s/column/s have equal sums, pick two and swap two elements from them. Since there are O(N2) possible sums and only O(N) are used, you can guess that this will give a solution quicker for large N.
That's a really weird solution, I've never seen something like that :D
Just one more question: in your code, that part with "if (N <= 11)", what does it do ?
Just pick random solutions until one sticks. You could probably remove that part and the code would still work, it's just what I wrote at first.
Note that it's quite easy to make every sums "equal", which is a complete reverse of given problem : You just pick any arbitrary permutation, and write down all of it's cyclic shifts in a rows.
After finding out this fact, I tried to pad some numbers to make those sums different. I first wrote down {2, 3, 4, .... N-1}, {3, 4, 5, .. N-1, 2} ... in rectangle [2, N-1] x [2, N-1]. Now I have 2 numbers of {2, ... N-1} and N numbers of {1, N}. I wrote 2 ~ N-1 to each row and column, and placed other 2N numbers appropriately to make all sums different. In result, it looks like this in N = 7 :
It's easy to show that it gives answer correctly from N >= 5. (code : https://cses.fi/95/result/40780)
Really neat solution. Thank you very much.