Topcoder SRM 708
→ Pay attention
Before contest
Codeforces Round 940 (Div. 2) and CodeCraft-23
37:46:24
Register now »
Codeforces Round 940 (Div. 2) and CodeCraft-23
37:46:24
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 2 | adamant | 164 |
| 4 | TheScrasse | 159 |
| 4 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/20/2024 03:48:37 (k2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










And all room winners get T-shirts: https://www.topcoder.com/blog/a-flood-of-love-hits-the-topcoder-community/
Did anyone receive their shirts for SRM 701?
Even for Div2? Why am I in Div1 :(
And I ended up second in the room.. RIP all who came second in room
I'm lucky :) Do I just have to set my address in the settings? What about T-Shirt size, didn't find any setting?
I don't actually send out the t-shirts, I just follow the news related to them :-) But you definitely have to set your address in your profile.
Contest will start in 36 hours!
Hour
Please, Someone explain his solution for Div 1 250 :)
My idea is to use only 3 characters to support up to 15 strings Like this: a, a ... a, bcbcbc....
Nice One. Thank you.
Solution for 500 ?
I used three DPs:
dpOut[i][j]means count of palindromes in substring (i .. j),dpOutReal[i][j]means count of palindromes in substring (i .. j) which strictly have ith and jth characters.dpIn[i][j]means count of palindromes in subsequence (0 .. i); (j .. n-1).Then, we choose
ifor which we want to calculatex[i]. Where can it be in the palindrome. Imagine the palindome:Let the last c will be our ith character. So, the inner part of the palindome will be
cdedc(it will have our ith element as one of its ends) and the outer part of the palindrome will beab baSo, let's iterate all possible inner parts. Let the beginning of inner part will be the x character, and the ending of inner part will be y (it's easy to see that
x = iory = i).Now, for that inner part there will be
dpOutReal[x][y]and to choose an outer part for it we will usedpIn[x-1][y+1] + 1(+1, beacuse we can have no outer part). Now, we'll add tox[i]dpOutReal[x][y] * (dpIn[x-1][y+1] + 1)WINNERS: rng_58, tourist, Petr, anta and Baklazan. Congratulations guys!
my codes: div2, div1-easy BalancedStrings, div1-med PalindromicSubseq, div1-hard OptimalBetting
div2-med: greedily try to insert strings with as big score as possible (but don't exceed the value of K)
div2-hard: dynamic programming in O(n2). Let
dp[i][j](i < j) denote the number of ways to choose subseqeunces of indices on the left from i and from the right from j so that they will be symmetric. At the end answers aredp[i-1][i+1]or something like that.div1-easy: First string can be ABABABAB..., the second CDCDCDCDC..., and each of other strings should consist of one letter only (from 'e' to 'z'). You can check that two first strings produce enough "instability".
div1-med: Two dynamic programmings: from inside and from outside. Let
dp_out[i][j]denote the number of ways to choose indices on the left from i and right from j so that they will be symmetric, and letdp_in[i][j]denote more standard dp: the number of palindromes in the interval [i, j].div1-hard: It turns out that the probability of getting to the goal amount of money (when playing an optimal strategy) depends on rounded value of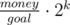 . A naive approach to the given problem is O(goal2·k) dynamic programming. The key observation is that values close to each other in one "interval" (interval defined by the same value of probability of winning in optimal strategy) have similar sets of optimal bets. If you divide numbers from 1 to goal into 2k "intervals", for each previous amount of money the set of good (got from optimal bets) new values in one "interval" is a smaller interval itself. A related fact mentioned earlier: the set of optimal moves from a and from a + 1 (where a and a + 1 are from the same interval) differ only by constant number of elements.
. A naive approach to the given problem is O(goal2·k) dynamic programming. The key observation is that values close to each other in one "interval" (interval defined by the same value of probability of winning in optimal strategy) have similar sets of optimal bets. If you divide numbers from 1 to goal into 2k "intervals", for each previous amount of money the set of good (got from optimal bets) new values in one "interval" is a smaller interval itself. A related fact mentioned earlier: the set of optimal moves from a and from a + 1 (where a and a + 1 are from the same interval) differ only by constant number of elements.
I think you have a typo in your div2-hard explanation:
"left from i and from the left from j"
should be from the right of j
Yes, thanks.
Why greedy works in Div2-med? What if we run into situation where we used 49 strings and we still need the score 53 (or any other prime number > 50)?
The biggest possible score of one string is 26·50 = 1300. You can use it at most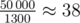 times. After using some multiply of 50 in the next string the remaining needed score will be less than 50 (otherwise we would use a bigger multiply of 50). Note that we can use a string with score that is not multiply of 50 but it can only make things better. Finally, in one more string we can get exactly the remaining needed score because it's less than 50.
times. After using some multiply of 50 in the next string the remaining needed score will be less than 50 (otherwise we would use a bigger multiply of 50). Note that we can use a string with score that is not multiply of 50 but it can only make things better. Finally, in one more string we can get exactly the remaining needed score because it's less than 50.
Thank you! I understood the first part with multiples of 50, but I couldn't understand why using a different number makes things better.
For example, this code doesn't use multiples of 50 as the last step. I thought that he was lucky before I saw that note. Does this code exhaust the K in the same way you've described?
We can use strings with scores that are not multiplies of 50. It's a possibility, not an obligation. An extra possibility can't make things worse. I don't claim that it's useful though.
That code uses big multiples of 26 and squares of numbers smaller than 26. It's slightly more complicated to prove its correctness but it indeed achieves any allowed K in at most 50 moves. You can analyze it this way: once you start decreasing a variable
len, how big can K be in the next step? And how big can it be in yet another step?REPORT
Admin please have a look into this http://imgur.com/CHav3o4
PS: I would like to know to how add a pic in a comment.
Maybe this is what you wanted :
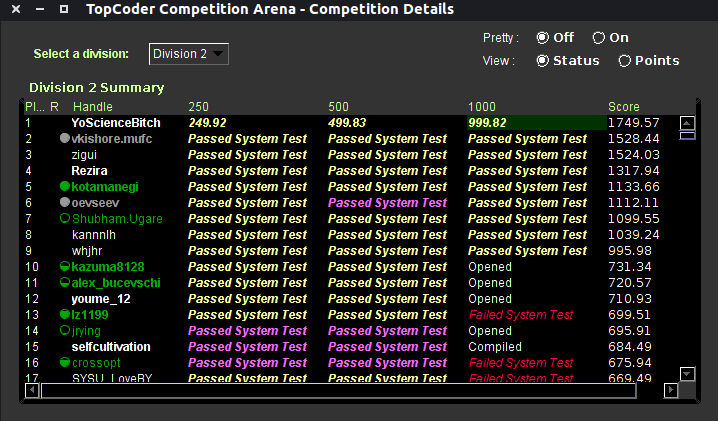
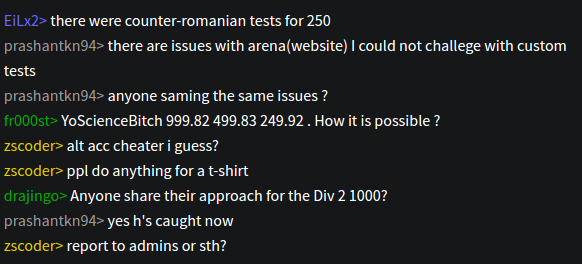
EDIT: Seems YoScienceBitch is here to stay RankList
I pity YoScienceBitch for having slow internet connection.
Maybe he thought that submitting 20-30 seconds later will make him look any less suspicious.
Can someone explain Div2-Hard in more detail? I don't completely understand the above explanation.
Thanks
Let dp(L, R) denote the number of palindromic subsequences you can choose in the range (0,L) U (R, N-1).
For each i, you need to calculate dp(i-1, i+1).
Now the recurrence relation. Divide it into cases.
Suppose you are at state dp(l,r) and decide to neglect str[l]. Then you move to state dp(l-1, r). If you reject str[r], you move to dp(l, r+1). Add both of these. But this induces double counting, i.e. when you reject both str[l] and str[r]. So subtract dp(l-1, r+1) from the answer.
Also, when str[l]==str[r], you can choose both and go to state dp(l-1, r+1), so add this value whenever applicable. :)
To sum up,
When str[l]!=str[r], dp(l,r) = dp(l-1,r) + dp(l, r+1) — dp(l-1,r+1)
When str[l]==str[r], dp(l,r) = dp(l-1,r) + dp(l, r+1)