Hi to all!
215A - Bicycle Chain
Because of small constraints we can iterate i from 1 to n, iterate j from 1 to m, check that bj divide ai and find max value of 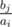 . Then we can start this process again and find amount of the pairs in which
. Then we can start this process again and find amount of the pairs in which 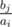 is max value.
is max value.
215B - Olympic Medal
Let amagine we have values of r1, p1 and p2. Then:
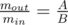
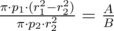
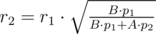
Now it’s easy of understand, we must take maximum value of r1 and p1, and minimum value of p2 to maximize r2. You could not use three cycles for iterating all values, but you could find property above about at least one value and use two cycles.
215C - Crosses
Let’s iterate n1 = max(a, c) and m1 = max(b, d) — sides of bounding box. Then we can calculate value of function f(n1, m1, s), and add to the answer f(n1, m1, s)·(n - n1 + 1)·(m - m1 + 1), where two lastest brackets mean amount of placing this bounding box to a field n × m.
Now we must calculate f(n1, m1, s). At first, if n1·m1 = s then the result of the function is 2·(⌊ n1 / 2⌋ + 1)·(⌊ m1 / 2⌋ + 1) - 1 (you can prove it to youself).
If n1·m1 > s then we must to cut 4 corners which are equal rectangles with square 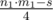 . We can iterate length of a one of sides, calculate another side, check all constraints and add 2 to the result of the function for all such pairs of sides.
. We can iterate length of a one of sides, calculate another side, check all constraints and add 2 to the result of the function for all such pairs of sides.
The time of a solution is O(n3), but it’s with very small constant, less then 1.
215D - Hot Days
You can use only two features about this problem: the solution is independenly for all regions and there are only 2 possible situations: all children are in exactly one bus or organizers must take minimum amount of bus such no children got a compensation. It’s bad idea to place some children to hot bus and to place some children to cool bus simultaneously.
For solving you must calculate this 2 values and get minimum.
215E - Periodical Numbers
Will be soon…











Why in problem D (Hot Days) you only need to consider the two situations mentioned? Thank you.
because the cost is a linear function about the number of buses
I also can't understand the solution
Supose that we will arrange n buses in ith city: If T[i]-t[i]>m/n , no children will get compensations.
If T[i]-t[i]<k/n , ans=cost[i]*n+{m-(T[i]-t[i])*(n-1)}*x[i] =cost[i]*n+m*x[i]-(T[i]-t[i])*n*x[i]+(T[i]-t[i])*x[i] ={cost[i]-(T[i]-t[i])*x[i]}*n+(T[i]-t[i])*x[i]
cost[i],x[i],T[i],t[i],m is known,and it's a linear function about "n".So the MinCost must appear on the endpoints.
Thanks a lot. I get it now :)
I didnt get the solution for Crosses. Here f(n1,m1,s) denotes the number of crosses that can be created with area s and n1 = max(a,c) & m1 = max(b,d). But why are we adding f(n1,m1,s).(n-n1+1).(m-m1+1) to the answer ?
Because we can additionally position the center of the cross in (n - n1 + 1)·(m - m1 + 1) ways on the given grid.
So will you write the solution for the last problem too?
Why the solution to problem E still hasn't been published?