Hi! I'll try to explain solution of problem E on Codeforces Round #132.
Ok, in the very beginning let's try solve some other task. We'll find the number of such integers in the interval (2k, x], where 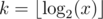 . And someone can see that x has length len = k + 1.
. And someone can see that x has length len = k + 1.
Then we should try blocks of {0, 1} to be the same part of periodical number. These blocks have length, which is divisor of len.
Let's calculate number g[i] of such blocks of length i, where i is some divisor of len. We get i of first(from the left side) bits of number x and name it as t = x >> (len - i), e.g. if x = 100110002, and i = 4 then t = 10012, if i = 2 then t = 102. Firstly, we should check block t, it needs for example to check number p = ttttt... repeated 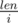 times, it can be calculated in a loop p = p << i + t. It's clear if p ≤ x, then we should take into account this block g[i] = 1. It's clear that every correct block less or equal than t, and it should begin from 1 (because of periodical number is without leading zeroes). Case of equality we took. And we should add to g[i] difference between t and 2i = 10000...2 i-1 zeroes, g[i] = g[i] + t - (1 << (i - 1)). It seems that all is ready and we can sum g[i] for every divisor of len and not equal len, but we cant. Because some cases we count more than once, e.g. x = 101011002, i = 4, g[4] = 1 + (10102 - 10002) = 3 we considered cases of blocks 1000, 1001, 1010, and when we count for i = 2,g[2] = 1 + (102 - 102) = 1, we considered one case 10, but 1010 is obtained from 10 repeated two times. But we can easily escape these problems, for this we should substract from g[i] all g[j] where j < i and j divides i.
times, it can be calculated in a loop p = p << i + t. It's clear if p ≤ x, then we should take into account this block g[i] = 1. It's clear that every correct block less or equal than t, and it should begin from 1 (because of periodical number is without leading zeroes). Case of equality we took. And we should add to g[i] difference between t and 2i = 10000...2 i-1 zeroes, g[i] = g[i] + t - (1 << (i - 1)). It seems that all is ready and we can sum g[i] for every divisor of len and not equal len, but we cant. Because some cases we count more than once, e.g. x = 101011002, i = 4, g[4] = 1 + (10102 - 10002) = 3 we considered cases of blocks 1000, 1001, 1010, and when we count for i = 2,g[2] = 1 + (102 - 102) = 1, we considered one case 10, but 1010 is obtained from 10 repeated two times. But we can easily escape these problems, for this we should substract from g[i] all g[j] where j < i and j divides i.
Some note. We get some DP problem, we calculate g[i] from i = 1 to the most divisor of len which is not equal to len, and update its value by substracting all g[j].
Let us summarize some ideas, we can count number of periodical numbers in the interval (2k, x], by going through divisors of len and calculating g[i], and then we return sum of g[i] where i < len and i divides len. One can see that 2k cant be periodical. Given this fact we will calculate this value for x = 2k - 1, then 2k - 1 - 1 and so on.In the end we get x = 1, and we get set of non-intersecting intervals, counting on each of them and sum up it we get answer. It can be done recursively. My code in C++, when I also precalculated divisors of each number from 1 to 60. I'm waiting for your replies and some criticism.









