We have a tree with n (2 ≤ n ≤ 1000) nodes and we need to find k (1 ≤ k ≤ 100 and k ≤ n - 1) vertices such that the path going through all of these vertices has the maximum length.
Note:
- The path should start at vertex
1and finish also at vertex1. - The algorithm has to return just the length of the maximum path (the path itself is not needed).
- The weight for an edge has following restrictions: 0 ≤ w ≤ 100000.
Let's say we have the following tree with n = 5 vertices: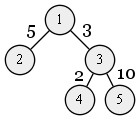
We need to find k = 3 vertices which will give us the longest path.
For this tree the maximal path is the following:1 ⟶ 5 ⟶ 2 ⟶ 4 ⟶ 1
It has the total length of 13 + 18 + 10 + 5 = 46.
So, for that particular tree we have to print 46 as our result.
I came up with a following greedy/dp-like solution. First we solve the problem for k = 1 and we remember this solution in a linked list 1 ⟶ v ⟶ 1. After that we try to solve the problem for k = 2 by trying all of the remaining n - 2 vertices and insert it in the current path: 1 ⟶ u ⟶ v ⟶ 1 and 1 ⟶ v ⟶ u ⟶ 1. After going through all of the vertices we choose the one which gave us the best result. Then we proceed to solve k = 3.
The problem is that it looks like this solution is not correct, because it fails the tests for this problem. I cannot prove that my solution is correct and I cannot disprove it. All I managed to do is to generate millions of different random trees and in all of these cases my clever solution matched bruteforce solution.
For now all my effort is directed towards generating a counter example in which my method will fail, but if it is correct I'd be glad to see the reasoning why is it correct.











Are all the k vertices required to be distinct?
You are correct. We have to choose k distinct vertices, but we are allowed to cross a vertex more than once while walking along the path.
In your solution, are you maintaining distinct vertices somehow?
Yes, I am maintaining the largest path that I currently have in the array:
And I maintain the vertices that are already in the path in the array:
Your method is greedy.
Suppose k=5, and you find the longest path 1->2->3->4 at k=4, now you can't choose these vertices again as targets. What if 1->2->5->3->4 is longer than 1->2->3->4->5 but 1->2->5 is shorter than 1->2->3 ?
This is actually the level of my current progress =)
I wasn't able to construct a real tree which fails this solution.
You are picking the longest path, and then back to 1, then the second longest and back to 1, third longest and so on, keeping in mind that you don't re-target a vertex. But you don't need to check 'back to 1' every time. Just reaching the target might be sufficient.
Maybe a simple fix like terminating greedy at k-1 iterations, and then checking kth iteration + path to 1 for every un-targeted vertex will work. But I'm not sure. I haven't proved it yet.
Is my solution wrong? If it is, how does the tree look like which fails my solution?
I don't know if I can help you find a test case right now ( I am sleepy ) but I think the order of choosing vertices matter. So if optimal order has 3 before 4, and
1->2->3 > 1->2->4but1->2->3->1 < 1->2->4->1, you choose1->2->4->1, therefore changing the optimal order.I mean, instead of checking 1->v->u->1, check only 1->...->v->u until k-1. At final k, check u->w->1.
Not proven. Just an idea. Good luck :)
Another idea : graph and k-cycle. Good luck :)
And let us know if you get AC :)
You should also consider cases where your candidate paths have equal values. As the order of choosing matters, we might make a mistake here.
This argument seems right, but a real tree that breaks this algorithm will help tremendously.
Looks like I have one :)
1 2 10
2 3 20
2 5 20
1 4 20
and k = 3
Your algorithm chooses as follows :
1->3->1 or 1->5->1 . Let's say it chose 1->3->1.
Now it has option 1->3->4->1 = 100 and 1->3->5->1 = 100.
Now your algorithm chooses one of these without any other criteria, but we can see that the optimal order is 1->3->4->5->1.
My algorithm returns the length of 160 for that tree: http://ideone.com/NO769r.
Is that correct?
Lol, yes! But only accidentally.
You must've chosen 1->3->4->1 instead of 1->3->5->1, but they have equal probability of picking by your algorithm. :)
The point is, your algorithm doesn't handle equal candidates well. I hope you get the point. I can't spend any more time on this :)
I added some debug lines in your code your code
The output suggests your algorithm doesn't do what you said it does.
max_path_length=60best_v=4 best_increase=40 max_path_length=100best_v=5 best_increase=60 max_path_length=160Case #1: 160If in the start, max_path_length=60, then when best_v=4, why is increase=40? Then when best_v=5, increase is 60? These values are not what I expected to see. Btw, the input for code is slightly different. I wanted to show that your code gives wrong answer on slightly changing the above example I gave.
I am spending my time on that, because it might be so that there has to made just a small incremental change and suddenly the algorithm becomes correct.
For example, Dijkstra's algorithm is also greedy, but it works because we are traversing all the vertices in the right way. Maybe if we always choose the correct vertex (among all of the vertices that give the path with the same length), the algorithm suddenly becomes correct =)
It does exactly what I said it does =)
The input is exactly the same as what you have suggested =)
Each line describes an edge:
parentweightparentweightNo, I changed the input.
Swap positions of 4 and 5, like here :
1 2 10
2 3 20
2 4 20
1 5 20
and k = 3
The input format is different than how I presented. So I made some assumptions about the input format. Try this modified example.
The result is 160: http://ideone.com/q2NzDS
Output using your algo should be :
max_path_length=60best_v=4 best_increase=40 max_path_length=100best_v=5 best_increase=40 max_path_length=140Case #1: 140According to your algo, answer is 140, which is wrong. According to your code, the answer is 160, which is correct, but your code != your algo.
Just try with pen and paper and you will see why this is the output for your described algorithm.
Your code is doing something else. Find the bug, and your algo will give wrong answer on this test case.
I can't find a bug: http://ideone.com/uQebyB
The algo constructs the paths like that:
1⟶3⟶1+ 601⟶4⟶3⟶1+ 401⟶4⟶5⟶3⟶1+ 60My code does exactly what I have described.
No. The distance between vertex
2and vertex5is 5 + 3 + 10 = 18....
I am sorry, I don't understand.
Are you talking about the edge
3⟶4?This is the only edge in this tree that has length 2.
Oh I confused path weights and vertex numbers. My bad.
solution forgetting about K below :((
I haven't managed to prove your solution wrong, but I think I found one solution I can prove. If it's indeed correct you could use it to find counterexamples for yours.
First let's find an upper bound on the maximum possible value of the sum. Analyzing each edge separately, it appears at most 2 * size(minimum_subtree_size) times in the path we are looking for, where minimum_subtree_size is the minimum size of the two subtrees formed when you delete that edge. Then summing that up for all edges, we get an upper bound on the result.
I claim that upper bound is attainable. Lets root our tree in a node such that none of the subtrees generated by its sons has size greater than n / 2, so each subtree has size less than or equal n / 2.
Then we can find a path (a cycle really, because we have to go back to node 1) where each pair of consecutive nodes in the cycle belong to a different branch of the tree. That path could be found greedly.
Moreover, by the property of the selected root, all edges will fulfill the upper bound from the first paragraph. So we have a solution.
I know this is somehow not very well explained, and there is certain probability of mistakes, so check it and let me know :)
How would you use K in your solution?
hahah that was what I was missing :) sorry for that, I don't really know how to use it :((
Not sure what you meant exactly, but is it this :
Make a graph with edge from each vertex to every other vertex and find the largest cycle of size k+1 in this graph starting and finishing at 1.
Here is a solution:
First, consider the problem where we do not need to return to the first vertex at the end. Then, one can notice that the optimal solution is to, at each step, visit an arbitrary farthest vertex from the current vertex (and mark the current vertex as visited).
The complexity of the solution to this problem is O(N * K)
However, now we can iterate over all possible ending vertices and perform the same algorithm. Total complexity would be O(N^2 * K).
Why is everyone downvoting? If there's something wrong with the solution, could someone explain what it is?
I have upvoted your answer, because I appreciate any involvement in solving the problem.
However, I don't understand your solution. Maybe that's the case for the others to downvote (but I'm not sure).
You could write the program and see if it'll be accepted on the online judge.
I'm not sure but isn't this the same as solving the TSP greedily?
Since for each node of the route we only care about the next node(I will call it matching a node with another one), now we can do this:
Dp[v][i][false,true]=the maximum lenght of a route in v's subtree such that we have i not matched nodes yet and true=the second node of the route is in this subtree/false=otherwise.
O(n*k^2)
How do you incorporate the fact that we have to go back to node 1 finally too ???
Dp[1][1][1]
Can you explain in more details?
How do you keep track of which nodes you have already visited? You might have to get re-enter a subtree a few times to increase the length.
managed to get a very large input where your solution fails (it's smaller than answer shown in udebug) https://puu.sh/uEbNc/f1d8e8f44c.in
Great! That is the first progress for the whole time and all what was needed is a little help of the red guy =)
Did you just generate a random tree or it has some special properties?
It is k=6 (or some near integers) chains attached to root 1.
You likely made some mistake in the generator/script. I have run your solution on hundreds of small tests and it was enough.
Your solution finds a path 1-5-2-6-1 with total length 24. The optimal path is 1-6-2-4-1 with total length 26.
(drawn with CS-Academy tool)
It looks like I had a bad generator.
Now, looking at this tree it doesn't seem to me that my algorithm can be cured, though I'll try to think about it a little bit more.
Well, what I notice is that this optimal path 1-6-2-4-1 can be built by looking for the furthest vertex from the current one. Again, I'm not sure that this will work in general =)
Now that's exactly what I said :PPP
This approach is easier to break. Consider a graph with edges: 1-2 of length 10, 1-3 of length 1, 3-4 of length 7, 3-5 of length 7. The optimal path is 1-4-2-5-1, while the greedy starts with 1-2-...
Checkmate =)
I have no more new ideas.
Wow, maybe we can run these 2 algorithms and choose the max between them? =)
root your tree in node 1
let us say there is an edge between node u and node v , if you choose to visit [ x ] nodes in the subtree of v then there is x nodes there and K — x nodes outside
then you will traverse the edge min(x , K — x) * 2 times if you behave optimally and you can proof that you can always do that
it turned out to be a normal knapsack on a tree
dp[node][visited nodes in its subtree]
call dp[1][K-1]
How to prove that number of traversals are min(x , K — x) * 2? It is easy for a line tree, but I am not so sure how to prove for a general tree(or extend it). Thanks in advance!
It's easy. If x > k-x then you will go outside the subtree k-x times, as after going outside k-x times, you have no more nodes to visit outside the subtree. The remaining x — ( k — x ) nodes are inside the subtree, so you will not go outside the subtree now. Similarly for x < k-x.
The Kth traversal is to the parent of 1(outside 1's subtree), and edge_cost(1,parent of 1) = 0. Is this right?
I still don't understand. In a knapsack problem we have a set of things which have 2 attributes: weight and value. What is our set of things and what are theirs attributes?
It's about distributing the nodes on subtrees.
the value is calculated as i mentioned above
BTW this is the "only" cool problem in all Arab Region contests :D
So your time complexity is O(N*K^2)?
If your answer is yes then I think it's not good enough (there are t<=100 test cases in the problem).
UP: My mistake. It's OK.
1) Why do we call dp[1][k-1] instead of dp[1][k] ???? 2) We traverse an edge min(k,k-x)*2 times ,but say all the k nodes lie in the same subtree ,Then the edge joining will be traversed (0) times ???? Please correct me if I got anything wrong . Thanks in advance..