Hello everyone!
I would like to invite you to participate in an upcoming HackerEarth contest — HackerEarth March Circuits. It's a long contest that will start on March, 17 21:00 IST (check your timezone). Contest will run for 9 days.
The problemset consists of 7 traditional algorithmic tasks and 1 approximate problem. For traditional algorithmic tasks, you will receive points for every test case your solution passes — so you can get some points with partial solutions as well. For the approximation task, your score depends on the best solution in the contest so far. Please check contest page for more details about in-contest schedule and rules.
I'm a tester of a problemset you'll have to work on. Thanks to harshil for preparing classic part of the problemset, to pkacprzak for preparing approximate task and to r3gz3n for handling technical part of contest preparation.
Tasks should not be very hard for top-level contestants, and I expect them to get full score on classic part of a problemset. However, even if you solved everything — you'll still have to do your best on approximate problem :)
As usually, there will be some nice prizes for those who'll reach top spots, here are prizes for top5 (in case you haven't open contest page):
- $100 Amazon gift card + HE t-shirt.
- $75 Amazon gift card + HE t-shirt.
- $50 Amazon gift card + HE t-shirt.
- HE t-shirt.
- HE t-shirt.
Upd. Contest has ended, approximate problem has been judged on final test data, all editorials has been published, all codes are public now.
Congratulations to winners:
1) mugurelionut
1) biginnnner
3) yzyz
4) ceilks
4) SkyFire











It was a Matrix's Circuits
Please provide more detailed editorials. harshil, I_love_Tanya_Romanova
They will be uploaded soon.
The solution provided in the editorial for "Submask Jumping" fails for this test case, 2047 2047 0
It uses 539648KB of memory whereas memory limit is 256MB. So tests were weak.
Link: http://ideone.com/1NrXbK
If this was the intended solution, please increase the memory limit and rejudge all the submissions for this problem. Thanks!
You mean the worst case of the official solution is just M=N=(2^11)-1? But it works fine for M=N=(2^22)-1? :) [I'm just asking, I haven't actually tried to run the official solution on any test case]
Anyway, rejudging all submissions seems like an extreme measure. I expect that most Accepted solutions use a very small amount of memory. For instance, my solution uses only O(BITS^2 + Q) memory, where I rounded BITS up to ~25.
The official solution uses (M + 1) * (N + 1) * (log(M) + log(N)) of ints which is nearly 23 * 2^23. But there is no test case where M * N is as large as 2^22. I looked at your solution, it's very good. If that was the official one, I have no problem at all. (maybe constraints would have been N * M <= 2^30 in that case)
The official solution passes all those tests because they were weak. My solution (same as official one) fails on those test cases just because I allocated 23 * 2^23 amount of memory in the beginning itself rather than using dynamic arrays.
I just want to let moderators know about this error. Deciding what to do next step is left to them.
This problem has a way more memory efficient solution with stirling numbers of second kind.
Note that if we neglect the obstacles, the number of ways to go from (a, b) to (p, q), where p is a supermask of a, and q of b is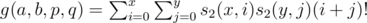 , where x is the number of 1 in a xor p, and y is the number of 1s in b xor q.
, where x is the number of 1 in a xor p, and y is the number of 1s in b xor q.
The logic for the formula is that we have to add a total of x ones to a, and y ones to b to reach (p, q). Say we take i steps in X direction and j steps in Y direction, then we can first make non-empty partitions in s2(x, i)s2(y, j) ways, and then permute them in (i + j)! ways.
First, we store the values of g for each x and y. This takes O(b2) memory and O(b4) time, where b is the maximum number of bits.
Now, if we sort the obstacles according to the pairs (xi, yi), and say f(i) is the number of ways to reach obstacle i, then:
Clearly, this solution uses only O(q + b2) memory, and O(q2 + b4) time.
Solution Link