Hello,
I was trying out this problem on Kattis, but I couldn't come up with an efficient solution. It seems like an interesting problem. Here is what the problem basically amounts to:-
Given N (N ≤ 1000000) points on a 2D Plane (0 ≤ xi, yi ≤ 1000000), compute 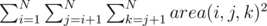 . Here, area(i, j, k) denotes the area of the triangle formed by points i, j, k.
. Here, area(i, j, k) denotes the area of the triangle formed by points i, j, k.
Can someone provide hints?
Thanks in advance.










Sorry this was for when the sum was over area(i,j,k). I didn't see that it was squared. I'm sorry.
Thank you for your response.
Yes, I figured out how to solve it for that as well. I couldn't quite extend it to sums of squares though and was wondering if there's a nicer solution altogether.
There is very messy way to do it. You can take each term and express it terms of coordinates of i, j, k. Then group up terms so that computation would be O(N).
Could you elaborate some more on your approach?
Sorry for the late post, but this method is perfectly feasible and gets AC. THe steps are extremely messy, but the result is beautiful.
First, express the answer like so:
[Extremely long expansion redacted]
Then, sum by parts, and reduce the nested sum into products of one-layer sums for each of the 21 summands:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
The result is
, and dividing by 24 gives
.
You need to use Python, though (intermediate steps go past the range of a 128-bit integer)
[Edit because math equation broke the page] [Edit 2: Latex Gods are not happy]
Nice username.
We can express the area of a triangle, given that its vertices are points (x1, y1), (x2, y2), (x3, y3) using the cross product. The formula we get is:
1/2 [(x2-x1)(y3-y1)-(x3-x1)(y2-y1)]
Let us solve the problem for a fixed (x1, y1) and (x2, y2), finding the sum of areas (not of squares of areas) of triangles formed by (x1, y1),(x2, y2), (x_i, y_i) for all i.
Rearranging the terms of the above area equation in order to have the variables x_i and y_i (note that I will be omitting the 1/2 in front, but don't forget to add it back in at the end).
x1y2-x2y1 + y_i(x2-x1) + x_i(y1-y2)
To get sum of all these areas, we can compute sum of all y values, let it be sum_y as well as sum of all x values. Let it be sum_x. The answer is now x1y2 — x2y1 + sum_y * (x2-x1) + sum_x * (y1-y2)
There is a problem with this approach however since the individual result we get from computing the area by cross product is that we can also get negative values. Adding up these values as we do here, withough taking the absolute value, will not produce the correct answer.
The question asks for sum of squares of areas, so the negatives we get will go away and we won't have to worry about this. To deal with squares we compute the square of the equation, getting
sq(x1) * sq(y2) + sq(x2) * sq(y1) + sq(y3) * sq(x2 — x1) + sq(x3) * sq(y1 — y2) — 2*x1*x2*y1*y2 + 2*y3*x1*y2*(x2-x1) + 2*x3*x1*y2*(y1-y2) — 2*y3*x2*y1*(x2-x1) — 2*x3*x2*y1*(y1-y2) + 2*y3*x3*(x2-x1)*(y1-y2)
Where sq(z) is z^2 (I just copied this from some code I wrote to test this, so I didn't change all of the symbols).
We proceed as last time, summing over all possible third point, having a fixed first two points. We will need to pre-compute the
These can all be computer in O(N).
Now, let us fix only the first point (x1, y1) and finding the sum of square of areas for all triangles (x1, y1), (x_i, y_i), (x_k, y_k). This is done using the result we have found above, and then performing another summation over k.
Something similar can be done to find sum of all triangles, summing over all possible first points as well.
Thanks for your response!
It seems that there is no nice and clean way to solve this problem.