Hello ! Can somebody explain to me how to solve this problem in O(logn) ?
Given N ( N <= 10^18 ) find the number of ordered pairs (a, b) for which a ^ b = X. ( 1 <= a, b <= N )
X is the first number >= N which has all it's bits equal to 1. For example if N = 5(101) then X = 7(111) and if N = 7 then X = 7.
Additional challenge : X is any number between 1 and 10^18, independent of N.
Problem link if somebody wants to submit : https://www.hackerearth.com/problem/algorithm/roy-and-maximum-xor/











Auto comment: topic has been updated by Ewwa (previous revision, new revision, compare).
Suppose a, b ≥ 0 instead; let 2p be the maximum digit of N.
Then X can't have any digits larger than 2p; if its maximum digit is 2p, then (w.l.o.g.) a must be ≥ 2p and b < 2p, otherwise (if it's smaller) a, b must be both ≥ or < 2p.
In all cases except a, b ≥ 2p, the smaller number is uniquely given by the larger one, so that's trivial. Otherwise, we can reduce the problem to X, N - 2p and solve that recursively. We have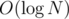 steps in the recursion and each of them can be solved in O(1), so that gives an
steps in the recursion and each of them can be solved in O(1), so that gives an 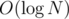 solution.
solution.
I dint understand why you got so many cases
Assume 2p <=N-1<2p + 1
So now the max possible number is 2p + 1-1. And number of ways is (N-2p)*2.
Since only one of them must be greater than or equal to 2p.Nowing if we fix that then other one is unique. So that gives the number of ways. With a corner case of N=1.
I am sorry if u are trying convey the same.I couldnt get it.
PS:I am talking abt the hackerearth problem.