Hello, Codeforces!
CS Academy will continue continue to host the online mirrors of Romania's National Selection Camps for IOI 2017. Round #6 takes place on Tuesday, 06 June 13:00 (UTC). The round will be unrated for all users. The statements will be available in English. If you want to take part in this round you need to register before the contest begins.
Contest format
- You will have to solve 3 tasks in 5 hours.
- There will be full feedback throughout the entire contest.
- The tasks will have partial scoring. The maximum score for each problem will be 100 points.
- There will be no tie breaker, so two users having the same total score at the end of the contest will share the same place in the standings.
If you find any bugs please email us at [email protected]
Don't forget to like us on Facebook, VK and follow us on Twitter.










any solutions to problem 2 without hashing?
How to do it with hashing?
idk but dotorya found n^1.5lgn hashing solution, by hashing I mean assigning random values to 1~1000000 and check subarray's validity with xor
That's how I solved it and it seems similar to arsijo's solution. Yes, there is some more complicated, fully deterministic solution, but I couldn't understand it in the few minutes I've talked to the author. The official solution had complexity O(N^1.5) with no extra log (even though, the hashing solution works in the same asymptotically time if you consider mapping to be O(1) as I usually do)
Ok I think I get it now.
Assign a random large value to each possible value in the range [1..1000000].
We'll determine that an interval [l..r] is good if the xor of all aj for all l ≤ j ≤ r which satisfies the condition that there exist an index k with l ≤ k < j so that ak = aj is 0. We call this xor value F(l, r) for convenience.
For each position i, let nxt[i] denote the next position with the same value as ai (if it does not exist, set is as ∞).
We can do a simple O(n) loop to compute F(1, i) for all i, and store them in some array, say f[i].
For each position l, we'll calculate the number of indices r such that F(l, r) = 0 quickly. To do so, we need to be able to update the values of f[i] after solving the problem for position l and also query the number of f[i] with i ≥ l and f[i] = 0 fast.
Note that after we finish processing position l, updating the values of f[i] is just xor-ing all values of f[k] with k ≥ nxt[l] by V[a[l]], where V[a[l]] is the hash value assigned to a[l].
Thus, we basically have to xor a suffix with a certain value v and find the number of 0s in a suffix. This can be easily done with sqrt decomposition on the array if we store a map of values of each block and also another value shift[i] for each block denoting that the whole block is xor-ed by the value shift[i].
Complexity :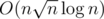
How to solve the third problem?
Can m log^2 n fit the time limit for first task?
In my case, yes.
Can you explain your approach? Please. Thank you. There is no editorial available online for this problem.
We use centroid decomposition like this :
I think this step is kinda typical for most tree divide & conquer problem. So let's see how to do step 3. Say that centroid is C and there is a son v1, v2, ..., vk. If a query (x, d) is derived from subtree of vi, then it is applied to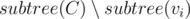 with value d - dist(x, C).
with value d - dist(x, C).
To make explaination easier we will just say it is applied to subtree(C) (it doesn't change significantly). We should sum up the value of max(0, d - dist(C, v)) for each vertex v. For fixed list can do it in O(lgn) time with binary search and partial sum.