First, I really need to apologize for the round. There was a serious problem in D that was even covered in the sample test, that the main solution did not handle correctly. I should have been much more careful with this problem and looked for these kind of cases. Unfortunately, it was a big enough issue that caused the round to be unrated. I know this upset a lot of people, but it's tricky to find a solution to this kind of problem after the problem has happened.
I still hope the problems were good quality. If you learned something new from the round, or from this editorial, then the round was worth it. I would advise to solve the problems you couldn't solve during the contest, so you can take away something from the round.
If you want any further clarification on a problem, please ask in comments!
821A — Okabe and Future Gadget Laboratory
We can simulate exactly what's described in the statement: loop over all cells not equal to 1 and check if it doesn't break the city property. To check if a cell breaks the property, just loop over an element in the same row, and an element in the same column, and see if they can add to give the cell's number. The complexity is O(n4).
Sidenote: The definition of lab here was actually inspired from a USAMTS problem in 2016.
The critical observation to make is that the optimal rectangle should always have a lower-left vertex at the origin. This is due to the fact that the line has positive y-intercept and negative slope: any rectangle which doesn't have a vertex at the origin could easily be extended to have a vertex at the origin and even more bananas.
Then, we just need to try every x-coordinate for the upper-right corner of the box and pick the maximum y-coordinate without going over the line. We can compute the sum of any rectangle in O(1) using arithmetic series sums, so this becomes O(bm) because the x-intercept can be up to bm. You can make it faster by trying every y-coordinate; this makes the complexity O(b), but this was unnecessary to solve the problem.
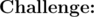 Can you solve the problem with better complexity?
Can you solve the problem with better complexity?
It looks like Daru should only reorder the boxes when he has to (i.e. he gets a remove operation on a number which isn't at the top of the stack). The proof is simple: reordering when Daru has more boxes is always not worse than reordering when he has less boxes, because Daru can sort more boxes into the optimal arrangement. Therefore, our greedy algorithm is as follows: simulate all the steps until we need to reorder, and then we resort the stack in ascending order from top to bottom.
This has complexity O(n2 log n). However, we can speed this up if we note that whenever we reorder boxes, any box currently on the stack can be put in an optimal position and we can pretty much forget about it. So whenever we reorder, we can just clear the stack as well and continue. This gives us O(n) complexity because every element is added and removed exactly once.
First, let's make this problem into one on a graph. The important piece of information is the row and column we're on, so we'll create a node like this for every lit cell in the grid. Edges in the graph are 0 between 2 nodes if we can reach the other immediately, or 1 if we can light a row/column to get to it. Now it's a shortest path problem: we need to start from a given node, and with minimum distance, reach another node.
Only problem is, number of edges can be large, causing the algorithm to time out. There are a lot of options here to reduce number of transitions. The most elegant one I found is Benq's solution, which I'll describe here. From a given cell, you can visit any adjacent lit cells. In addition, you can visit any lit cell with difference in rows at most 2, and any lit cell with difference in columns at most 2. So from the cell (r,c), you can just loop over all those cells.
The only tricky part is asking whether the current lit row/column should be a part of our BFS state. Since we fill the entire row/col and can then visit anything on that row/col, it doesn't matter where we came from. This means that you can temporarily light each row/column at most once during the entire BFS search.
So complexity is O(n + m + k), with a log factor somewhere for map or priority queue. Interestingly enough, you can remove the priority queue log factor because the BFS is with weights 0 and 1 only, but it performs slower in practice.
You can see the code implementing this approach below.
Another approach to this problem was using "virtual nodes". Virtual nodes are an easy way to put transitions between related states while keeping number of edges low. In this problem, we can travel to any lit cell if its row differs by <=2, or its column differs by at most 2, but naively adding edges would cause O(k^2) edges.
Instead, for every row, lets make a virtual node. For every lit cell in this row, put an edge between the lit cell and this virtual node with cost 1. We can do something similar for every column.
Now, it's easy to see that the shortest path in this graph suffices. A minor detail is that we should divide the answer by 2 since every skipping of a row or column ends up costing 2 units of cost.
821E — Okabe and El Psy Kongroo
You can get a naive DP solution by computing f(x, y), the number of ways to reach the point (x, y). It's just f(x - 1, y + 1) + f(x - 1, y) + f(x - 1, y - 1), being careful about staying above x axis and under or on any segments.
To speed it up, note that the transitions are independent of x. This is screaming matrix multiplication! First, if you don't know the matrix exponentiation technique for speeding up DP, you should learn it from here.
Now, let's think of the matrix representation. Since the x dimension is the long one and the y dimension is small, lets store a vector of values dp where dpi is the number of ways to get to a y value of i at the current x value. This will be the initial vector for matrix multiplication.
Now, what about the transition matrix? Since our initial vector has length y and we need a matrix to multiply it with to map it to another vector with length y, we need a y by y matrix. Now, if you think about how matrix multiplication works, you come up with an idea like this: put a 1 in the entry (i,j) if from a y value of i we can reach a y value of j (i.e. |i - j| ≤ 1). Don't believe me, multiply some vector times a matrix of this form to see how and why the transition works.
You can then build this matrix quickly and then matrix exponentiate for under every segment and multiply by the initial vector, then make the result as the new initial vector for the next segment. You should make sure to remove values from the vector if the next segment is lower, or add values to the vector if the next segment is higher. This gives complexity O(nh3 log w) where h = 16 and w = k.










Auto comment: topic has been updated by send_nodes (previous revision, new revision, compare).
Can ternary search be applied in B?
are you talking about using ternary search to find the rectangle with maximum area? I tried it at first , but I don't think maximum area here will maximize the result
Actually not. Let f(x) = number of bananas for rectangle with sides (y, mb -my). So i was thinking if this function is unimodal or not.
yes ternery search can be applied on problem B here is the link http://codeforces.com/contest/821/submission/28031950
Yes, it is what i was thinking about, thank you!
But how can we prove that ternary search can be applied on this function?
It's cubic.
In (x, y) we get (y+1)(x+1)(x+y)/2 bananas. Since y=-x/m+b It is cubic. Finding the maximum of the cubic in range can be done fast. It has three intervals, where it is increasing or decreasing.
Then i think we can just take a derivative of this function to find it's maximum and it will be O(1) solution. Nice.
Derivative contains square roots, so it is still O(log(m + b)) Check this link: [Derivative set to 0 wolfram](https://www.wolframalpha.com/input/?i=solve(d%2Fdx(+(x)(x%2B1)((-x%2Fm%2Bb)%2B1)%2B((-x%2Fm%2Bb))((-x%2Fm%2Bb)%2B1)(x%2B1)))+%3D+0)
Really, thanks
But ternary search is still much easier.
That is the real question, even I do not know the proof, but it works!
you can generally write the area in terms of x and y coordiantes as A = ((x+1)*(y+1)*(x+y))/2 --(1) now from equation of line x=b*m-m*y; put value of x in equation 1 and than value of A will be in terms of y only now find the second order derivative of A it will be less than zero for that range of y hence the graph will be concave downwards hence ternary search can be applied
Why cannot I apply binary search then? And why ternary? Can I get link to some article which explains this thing better. This the third question I have encounter in past 1 month, where binary search doesn't work, but ternary works!
yes binary search can also be applied for that after finding mid we will find area for that value and for mid+1 if area found at mid+1 is less than area found at mid than r=mid-1; else l=mid+1;
i don't understand programming very well, why would ternary search ever be better than binary?
because ternary gives you a complexity of log3N and that is better compared binary search complexity log2N
Actually ternary search doesn't give you a better time complexity (as you discard only 1/3 of the range instead of 1/2 of it in binary). The main advantage is that ternary search could be applied to more scenarios (eg: quadratic function) compared to binary (which must only be applied to a linear functtion).
Oh I didn't know that. But can you explain one thing that in ternary search we have two mid and we check three conditions (i.e. three partitions) so we choose only 1/3 and reject 2/3. This results to finding a solution everytime 1/3 of previous one so total steps are log3N. Please correct me if wrong.
we actually reject 1/3 leaving 2/3 on search space.
Please have a look at this code. In this code we have two mid1 and mid2 they trisect the whole array. Every time we search the whole array we divide in three parts and take that part in which our answer lies that is
The code you just show only applies to linear function, and IMO it's just a modified version of binary search.(though I see some people still refer it as ternary)
The ternary search we are talking about is the one which discards the segment of x which max/min y will not appear due to f(x) being quadratic. (Or linear)
Ok I will search about ternary search. Thanks for clearing my misconceptions:)
https://www.hackerearth.com/practice/algorithms/searching/ternary-search/tutorial/
This is Ternary's tutorials of Hackerearth, and it is similar to your description
Can you please tell me site or resource where i can find this concept. I tried to search it but not getting the required results Thanks again.
Check my comment here :) Sorry for my slow response
http://codeforces.com/contest/821/submission/28032851
This Knack's solution used ternary search.
I'm not clear about ternary search but is it not binary search?
it's similar to binary search, but it will divide searching range to 3 pieces. You can read more about it here https://www.hackerearth.com/practice/algorithms/searching/ternary-search/tutorial/
I'm not sure about ternary search's purpose. If you read the HackerEarth's tutorials above, you can see that it's like binary search which find a value in a sorted array. But if you read about ternary search at here: https://alexli.ca/A3C5.pdf, it describes ternary search: "Given a unimodal function f(x), find its maximum or minimum point...".
And sorry for my bad english :)
Hi[user:anhtan] ! A big thank you for sharing https://alexli.ca/A3C5.pdf. I saw this book for the first time and I think it is pretty awesome. Do you have any more material like this that we ( Novice coders ) can learn from. Thanks!
It's only english book that i know. But if you are finding something like this, i suggest you http://www.geeksforgeeks.org/. Geeksforgeeks have many algorithms with tutorials from basic to advance which is not hard to learn for the beginners.
How to solve D?
My solution to D in a word: discretize, build virtual points for each row and column, build graph, and the answer is the shortest path. (notice that the destination may not be lit) The complexity is O(n + m + k). (my submission uses
mapandpriority_queueso it may have a higher time complexity)How did you reduce the number of edges ?
I said "build virtual points for each row and column", so the number of edges is just O(n + m + k)----each (real) point can only have edge to/from up to 4 adjacent points, up to 3 rows(virtual points) and up to 3 columns(virtual points).
There's no edge from a virtual point to another virtual point, so the number of edges from virtual points is not greater than the number of edges to real points. So the number of edges = (edges from real points) + (edges from virtual points) ≤ (edges from real points) + (edges to real points) = O(n + m + k).
Just realised what you meant. Quite an ingenious approach !, I was'nt even thinking in the direction of virtual nodes. Just out of curiosity of developing the intuition behind something like this, did you think this on the spot or had you encountered a similar strategy in some previous question ?
I've encountered a similar strategy in some previous question:)
can you explain your approach bit more , like which real point to join with which virtual point and with what cost
Only edges from real points to virtual points have a cost of 1.
maybe you can check my code... 28036500
thanks:)
For b use wolfram: https://www.wolframalpha.com/input/?i=d%2Fdx(+(x)(x%2B1)((-x%2Fm%2Bb)%2B1)%2B((-x%2Fm%2Bb))((-x%2Fm%2Bb)%2B1)(x%2B1)))%3D0 Find closest x's in range. Done :D O(¹)
https://www.wolframalpha.com/input/?i=solve(d%2Fdx(+(x)(x%2B1)((-x%2Fm%2Bb)%2B1)%2B((-x%2Fm%2Bb))((-x%2Fm%2Bb)%2B1)(x%2B1)))+%3D+0)
can you explain it ?
First you have to realize that the number of bannanas in an area x by y is (x+1)(y+1)(x+y)/2. Also, y = -x/m+b. Substitute in and use calculus to find maximum value.
number of bannanas in an area x by y is (x+1)(y+1)(x+y)/2 how you come up with this ?
It's hard to explain without a diagram or picture and the editorial does not really explain. It just says "We can compute the sum of any rectangle in O(1) using arithmetic series sums". I'll try my best to explain. Look at this figure.
5 6 7 \n 4 5 6 \n 3 4 5 \n 2 3 4 \n 1 2 3 \n 0 1 2 \n
This represents how many bannanas are in each tree for a 3 by 6 rectangle. Notice the sum of the leftmost column is 5*(5+1)/2 from the formula n*(n+1)/2. The middle column is the same thing but every term is increased by one. There are 6 terms, so it is 6 + 5*(5+1)/2. Using the same logic, the next column is 12 + 5*(5+1)/2. These three columns together give 3*(5*(5+1)/2)+6+12, or 63. Now let's try to generalize for any x and y
y y+1 y+2 ... x+y \n y-1 y y+1 ... x+y-1 \n y-2 y-1 y ... x+y-2 \n ................................... \n 0 1 2 ... x \n
The sum of the left column is y*(y+1)/2. The sum of the second column is y*(y+1)/2 + (y+1). The third column is y*(y+1)/2 + 2*(y+1). This goes on until the last column which is y*(y+1)/2 + x*(y+1). Adding up all x+1 columns gets you (x+1) * y*(y+1)/2 + x*(x+1)/2 * (y+1). This simplifies so (x+1)*(y+1)*(x+y)/2.
Thank you! This really helped me out!
Can anyone tell why my solution to problem C got TLE? 28030270
I think it's of O(n.log(n))
I believe your solution is O(n²lg(n)).
Sort is nlogn. Your solution is O(n*nlog(n)).
yes, worst case is O(n^2 logn).
No, it is in fact O(n^2.log(n)). You are doing an O(n.log(n)) sort inside an O(n) loop.
But won't any of the n-items be sorted once?
So in total it will be O(n + n.log(n))? or I'm missing something?
O.S.Mozes lolzano ankeshgupta007 legoBridge
In the worst case, you'll have to sort after every remove. This can be achieved by alternating lots of messed up adds and one remove. You end up sorting O(n) times. This makes your algo O(n²lg(n)).
If it was the case that I need to sort after every remove command then the stack to be sorted will be of size 1, having almost no effect to the complexity.
Please note that I'm having two stacks and that I clear stack1 after every sorting process.
I said by altering many adds and only one remove . The stack will have a size greater than 1.
There are only n-adds & n-removes, after any sorting process I clear the stack. So every element that have been sorted will not be available in the stack for further sorting.
You are copying a lot of data between your two 'stacks'. Consider this test case:
On each removal, you would copy at least 150000 elements from stack2 to (the end of) stack1.
Yup I got it and reused double ended queue instead. Thanks a lot.
Will this tasks be in gym? And when? The previous one wasn't add and this is bad not only for me
Problems from regular Codeforces rounds are not added to Gym. And there's absolutely no need to, you can just go to the link of the original problems and submit your solution.
C is still unclear to me. "So whenever we reorder, we can just clear the stack as well and continue" — could someone explain this to me?
Anything on the stack can be reordered into the optimal order such that we don't need to spend any more reorders on them. So we can just forget about them and go on.
Whenever you need to reorder (ie, the top of the stack != needed element from 1 to n), you reorder the whole stack and put all elements in their optimal place. After this there are two cases:
The elements you add afterwards are correct in order: In this case it's obvious you are done.
The elements you add afterwards are not correct: In this case, you will encounter another need to sort, and by doing so, you implicitly sort the entire stack that has been cleared before and refine the order, then you can clear the stack again.
Here is my code
can you please help with this http://codeforces.com/contest/821/submission/28042330
getting WA on test case 9.
Here check out this case and analyze what your solution actually does wrong:
10 add 9 add 10 add 4 add 3 add 2 add 1 remove remove remove remove add 8 add 7 add 5 add 6 remove remove remove remove remove remove
Can you please explain that what if it's like this 5 add 2, add 8, add 12, remove, add 4, add 3 , remove, remove, remove, remove, I mean to say that what we cleared from stack (i.e. stack looks like 2 8) Now we expect that if there comes condition of rearranging we implicitly sort the whole stack but what if new additions are in order in themselves but not if we consider the whole stack till now ,like in this case. Please help!
http://codeforces.com/contest/821/submission/28040965 — this is my submission to problem D, WA 14 (48 + 49 later on), differences between my solution and tests are quite big (3 to 6, 4 to 20), can anyone take a look and maybe see what's wrong? Edit: I made a super wrong assumption, AC now.
Can you share your approach for the problem D?
Sure! In a BFS, in each layer (first layer starts from (1,1)) I visit all lit cells I can go to without having to lit any column/row (so those that form a path), and meanwhile I remember all columns and rows I visited during this BFS. When my queue gets empty, I've either:
Thanks!
Hey! Can anyone tell me why is this solution for Okabe and Boxes wrong?
Why my solution in D fails: Solution
You can get your solution to pass if you make sure to light every row/column at most once during your entire BFS like I mention in the editorial. Right now, it's inside your loop, slowing your program a lot.
Problem B is classical "Largest Rectangle in a Right Triangle" problem. https://www.youtube.com/watch?v=UzftAa_sXYs And I guess the solution with better complexity mentioned by the author implements this idea.
i did same but got wrong answer on testcase 4
In general, if a rectangle goes up to the integer coordinates (x, y) then we must count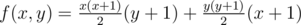 bananas. Maximizing the area would work if we had that
bananas. Maximizing the area would work if we had that 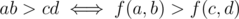 , however, consider a = 10, b = 73, c = 95, d = 7. We have that ab = 730, cd = 665, but f(a, b) = 33781 and f(c, d) = 39168.
, however, consider a = 10, b = 73, c = 95, d = 7. We have that ab = 730, cd = 665, but f(a, b) = 33781 and f(c, d) = 39168.
A possible intuition on this would come from observing that the area function is "quadratic" and the banana sum function is "cubic" in terms of amount of variables multiplied together. These functions are very unlikely to grow together in the general case.
The problem with this idea is that the problem is not looking for the rectangle with largest area. Actually, the solution could easily have a smaller area than the rectangle with largest area. For example, the rectangle formed between (0,0) and (1,5) would have more bananas (36) than the rectangle formed between (0,0) and (2,2), (only 18) even though it has less area. You are thinking that each node contributes the same number of bananas, but if you read carefully, you see that it is not true.
please help http://codeforces.com/contest/821/submission/28042958 This is my code for C. As you can see, in test 2 it fails (my output is 1 and ans is 2). BUT, when I run code myself I get correct answer (2) ! c++11 in codeblocks..
On your compiler array cisco is probably set to false automatically, you need to do it yourself on CF compiler though. After setting all array fields to false your solution fails on test 9.
Thank you so much! I cant believe you looked my code and helped me :D
I know about alternative solution for B with ternary search. It's okay, but I'm confused with the barriers when the search has finished. I think that I should consider only [left — m; right + m] to find the answer, but I have WA because of small range of my selection. So, maybe someone can help me with finding good barriers when the search has finished. My code — http://codeforces.com/contest/821/submission/28042340
For example, when I use [left — 1e5; right + 1e5] I have full solution, but if someone knew a more accurate borders it would be great.
The barriers should be left: 0 because that is the x-coordinate where the line intersects the y-axis; right: m*b because that is the x-coordinate where the line intersects the x-axis.
It's obviusly. You wrongly understood me, my fault. I want to know final barriers that I should consider after using ternary search. You said about barriers at the start of search. Check my solution, please.
For example, it's full solution — http://codeforces.com/contest/821/submission/28043315 , you can compare it with my wrong solution above.
Auto comment: topic has been updated by send_nodes (previous revision, new revision, compare).
Can D be solved with this approach: For every row and column store minimum cost from (0,0). Then x from 0 to n and y from 0 to m (if it's lit) (x, y)=min( min(row(y-1), row(y-2), col(x-1), col(x-2) min(row(y+1), row(y+2), col(x+1), col(x+2), row(x), col(y))+1,(x-1,y),(x,y-1))
DP doesn't work here because the recurrence might have cycles because we can walk on connected components of lit cells. Usually when the recurrence has cycles, you should immediately look at a BFS or DFS solution like the one in the editorial.
Note: I'm assuming you mean a DP like approach. If not, that's a totally different issue :)
Oh, yeah... :D my solution timed out, i think, what i needed map to store minimum cost in row/column.
Note: Yeah i was thinking about DP.
Could someone point out the mistake http://codeforces.com/contest/821/submission/28043433 ??
There might (and there is) a test, in which you do not clear stack when you should, which leads to additional increments of ans.
Problem c:
add 1 remove add 2 remove
why he need 1 time to reorder ?Does he need to reorder in this case ?
In this case, you don't need to reorder anything.
Clearing the stack will take O(n) time in worst case,which makes your algorithm O(n^2) worst case. A better approach will be to store the length of corrected size of stack in a counter variable. Correct me if I am wrong!
It takes time equal to the number of items on the stack. Since every element is pushed once and popped once, the amortized time complexity is O(n).
I got you!
I can't figure out why the 4th test case answer is 3 and not 4 for problem D. The note says that Okabe pays only when moving to (1, 2), (3, 4), and (5, 4). But what about when he moves to (2,3) or (3,2)? Why does he not have to pay then?
He can light the columns 2, then 4, then 5.
Okay I did not realize that he could light columns he was not on. But if he can do this, why can't he just light col 2, move to (3,3), and then light col 4? This would only take 2 coins.
Because he has to lit column or row 5.
I agree with you because it makes sense, but I've carefully read the problem statement several times and it does not say he has to light the final cell, just that he has to 'complete his walk'. I mean you can assume that he wants his lantern back at the end, but that just seems a bit too iffy you know
But to complete his walk he has to get to the corner, and to step on that cell he needs to get it lit, otherwise he cannot move there
Oh, I get it now. Thank you for your help!
How to prove the upper bound of the number of edges in D?
There's 4 edges to adjacent cells from every (r,c) cell. That's O(K).
Then, since we light each row and column once in total, all K cells get visited twice, so the amortized complexity of this part is O(N+M+K).
I am having difficulty in understanding E, how can we apply matrix exponentiation , someone plz explain in detail , i m naive to these type of questions, what exactly does the matrix exponentiation give ??
You should read this first to understand the technique!
Thank you very much i can't send nodes but i send lots of love and thanks to the codeforces community and it's users :)
4B — "There are no trees nor bananas in other points" — what is the purpose of this sentence? Clearly there must be bananas and tress at other points, else the problem doesn't make sense?
The problem states that, for every non-negative integers x and y, there are bananas at the point (x,y). Now, we need to know about all the other points of the plane: are there bananas at points (-1,-1) or (0.1,0.1), for example? This sentence you transcribed tells us that there are not, it is a necessary information for solving the problem.
I am quite surprised that problem D has a 4s TL when there exists an O(n+m+k) solution, when I saw the 4s TL and k <= 10^4 constraint I just simply lowered my guard and embraced O(k^2) without optimizing building edge between the lights.
My code with SPFA
Can you explain your approach for problem D?
I did pretty much the same thing others did, but instead of checking the accounting nearby columns and rows only once I bruted all of the nodes in each SPFA iteration.
The SPFA is guaranteed to run in O(k^2) due to the nature of the graph.
For the link that you gave for E, https://www.hackerrank.com/topics/matrix-exponentiation, how is the number at (0, 0) the required valued in the exponentiated matrix directly ?, don't we need to do matrix exponentiation and then multiply the resultant matrix with the initial value column vector to get the required value ?
For problem D. In addition, you can visit any lit cell with difference in rows at most 2, and any lit cell with difference in columns at most 2 ? Can someone explain why?
Imagine you have a lit cell in column x and a lit cell in column x + 2. You can light column x + 1, jump from x to x + 1, move up/down and then step onto the lit cell in column x + 2. Same applies to rows.
Thanks!
Please, can you not use define in editorial? It do code more unreadable.
Can anyone explain me that why in problem D, the sample data #4 outputs 3?
According to my understanding to this problem, it should be -1
In the sample data explaination, it literally says paying when moving to (1, 2), (3, 4), and (5, 4).
But how could u go to (3,2) without paying 1 coin to light all the cells in col #2?
We can light second column, do a route (1,1) -> (1,2) -> (2,2) -> (3,2) -> (3,3), then light a 4th column, go to (3, 4), (4, 4), then light a 5th column and go to (4, 5), (5,5).
but it says "To change the row or column that is temporarily lit, he must stand at a cell that is lit initially"
does this means that u have to stand on the spot that u read from the input or u can stand on the spot that is currrently lit?
Read from input, here we light rows columns being on 1,1 3,3 and 4,4.
I'm too could not understand during contest.
Red line — our moves. Yellow fields — lights. Green fields — our lights.
So we used 3 coins
thanks a lot, i get it. :)
My O(1) solution for the problem B
I really want to know how sqrt function works in O(1)?
in B you need to make solution faster O(b) if you use python. My solution on python O(mb) can not pass.
My D solution that works in O(k^2 * log(k)) got MLE in test 28. Then i replaced int with unsigned short and it's AC in less than a second :D 28057357
So my solution takes up to k^2 memory. I think that if it wasn't intended to pass, memory limit should be more strict.
My solution for D is slower than the expected solution, it is O(k^2). I am describing it below since I could not see any comment mentioning the same method.
Make connected components of lit cells and now do a BFS from the component in which (1, 1) belongs. The edges between components in this BFS can be determined by seeing the seeing whether we can join the 2 components by lighting a single row / column.
The memory used is less, i.e O(k) but time complexity is O(k^2).
Sorry, I misunderstood what you were running BFS on :)
In question E ,How are transitions independent of x ???
I was going to ask that, and I also don't understand how do I deal with linear recurrences in 2D, I am aware of how to use matrix expo for 1D linear recurrence but isn't it 2D? send_nodes
I've just put a lot more detail into the E editorial, let me know if you would like more explanation :)
What I mean by independent is that for given y, the transitions are always the same no matter the x.
so if we were to write the naive dp we can make a 2d array dp[2][16] and according to current x is even or odd we can make the transition from x-1(iteration). But can we code a recursive function and memoize in such cases(how to memoize)? In recursion I need a base case when x == k right but x is otherwise a redundant parameter (if I am correct). Thanks
can anyone explain question e matrix formulation proof
I dont understand solution for D. We make nodes only for lit cells?
yes!! but consider corner cases
RE: 821B — Okabe and Banana Trees — Challenge: Can you solve the problem with better complexity?
The following is an O(1) algorithm for solving the problem, implemented in GNU C++14.
http://codeforces.com/contest/821/submission/28066366
can someone pls look into my code? it's similar to one in editorial but with few changes. i think the problem is in handling case when lower-right cell is not lit. but i can't figure out what's wrong.
Edit: nvm, there was bug in my code, a stupid bug. here is AC code