I noticed that there existed a method to solve Codeforces 827A/828C like this:Submission
It ran really fast that it became one of the quickest solutions to this problem.However,when I opened the code,I found it was just a naive implemention only with some optimizations.
But if I gave the following data:
N=1000,
all the 1000 queries have the same string with length 1000 and k=1000,
the following numbers are 1,1001,....,999001,1000000,
the sum of all ki is 10^6 and the sum of string length is 10^6,which satisfies the data range.
In this condition,the code will have up to 10^9 times of calculation and I don't think it can pass within 2 seconds.
So can anyone please if it's the expected solution to the problem? Thanks!










Auto comment: topic has been updated by Marco_L_T (previous revision, new revision, compare).
I did it in (max value of ki + size of string ti corresponding to it)*log(sum of all Ki)
Lets define L as answer length. L ≤ 2·106.
Lets omit some task details and solve the following problem: You need to generate two sequences si, ki of length n, where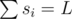 ,
, 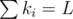 and ki·si ≤ L, maximizing
and ki·si ≤ L, maximizing 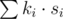 .
.
Given that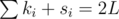 , ignoring the additional constraint on individual sequence's sum, to maximize product with a fixed sum of ki + si you need too make them as close as possible.
, ignoring the additional constraint on individual sequence's sum, to maximize product with a fixed sum of ki + si you need too make them as close as possible.
Now that should be obvious (but I'll still try to briefly cover this) that if you takeaway 1 from pair with maximum sum to add 1 to pair with minumum sum, then answer will not decrease if (and only if)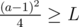 , otherwise the opposite inequality is held.
, otherwise the opposite inequality is held.
Want to prove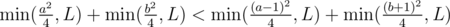
Is tantamount to
Is tantamount to
Which should be obvious
Backwards proof is almost identical.
That being said, we know that all sums ki + si are either equal to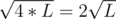 or there is at maximum one term which is not equal to zero. Now it is obvious that in the hardest testcase there are at most
or there is at maximum one term which is not equal to zero. Now it is obvious that in the hardest testcase there are at most 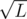 terms with each term being less than L.
terms with each term being less than L.
I guess that your example is exactly the test I came up with, but to briefly cover L1.5 testcase in one line: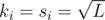
My 28455482 has the complexity of O(n + sum_of_k + res_sz).
This should fit the test given above.