Problem link: https://uva.onlinejudge.org/external/116/p11651.pdf . I know how to convert it to matrix exponentiation, On my solution the matrix is 77*77 size. as there are 200 test case and the matrix may be powered to 10^9 , It will case time limit exceed though O(n^3log(m)). How to make it time efficient ??
Rating changes for last rounds are temporarily rolled back. They will be returned soon.
×
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3640 |
| 2 | Benq | 3593 |
| 3 | tourist | 3572 |
| 4 | orzdevinwang | 3561 |
| 5 | cnnfls_csy | 3539 |
| 6 | ecnerwala | 3534 |
| 7 | Radewoosh | 3532 |
| 8 | gyh20 | 3447 |
| 9 | Rebelz | 3409 |
| 10 | Geothermal | 3408 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 163 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/24/2024 07:53:05 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










As far as I understand your solution work like this: you have some matrix A and vector v which depend only on the base and you need to calculate An·v for different n. When you use fast exponentiation, you find A2k for all k up to logarithm, multiply some of them and then multiply it by v. We can do the same, but in different order. Let's precalculate all A2k. Now instead of O(n3) matrix multiplication we can use O(n2) matrix by vector multiplication. We need to multiply matrices by vector, so time complexity is
matrices by vector, so time complexity is 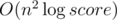 per query and
per query and 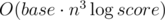 for precalc.
for precalc.
Btw why 77? I got 100 and i can optimize it to 50.
Sir , my solution may be wrong . Please explain your solution . I tried to solve reading a topcoder forum.
https://apps.topcoder.com/forums/;jsessionid=0CA65844DD4F4D178DAC03D867E65297?module=Thread&threadID=659037&start=0&mc=2#1177684 I didn't understand that totally. So i may be wrong . Sir please explain totally so that i can understand.
Denote by cntn, d the number of ways to get the score n if the last digit is d. Let's analyze the small case: d = 3. We have recurrence relations:
cntn, 0 = cntn - 1, 1 + cntn - 4, 2
cntn, 1 = cntn - 1, 0 + cntn - 1, 2
cntn, 2 = cntn - 4, 0 + cntn - 1, 1.
Do you know how to convert usual recurrence relation (like Fibonacci numbers) to matrix expo? Here we can do almost the same. Let's define a vector vn = (cntn, 0, cntn - 1, 0, cntn - 2, 0, cntn - 3, 0, cntn, 1, cntn, 2, cntn - 1, 2, cntn - 2, 2, cntn - 3, 2). These relations mean that vn + 1 = Avn for some matrix A, so vn = Anv0.
Sir, I know how to convert usual 1D recurrence relation to matrix (Like fibonacci). But it seems 2D, However I will try my best to convert it to matrix . But if i can not I will ask you.
If i can not do it and ask you please give me the answer.
Sir please answer me ,I have a problem . The matrix size is 100*100. How to optimize it ?? for last value 0 and 5 we have to keep 25 previous value each. . for last value 1and 4 we have to keep 16 previous value each. . for last value 2 and 3 we have to keep 9 value each. . so we have to keep total 25*2+16*2+9*2=100 value . . So matrix size is 100.
As there will be 200 test case and the power may be done upto 10^9 ,it will cause TLE.
You said you got 100 and optimized it to 50 , Then please explain. . . Another way you said is pre calculating. Ok i will precalculate all A^2^k matrix. But after that how it become O(n^2) ??
Let score =16, So I precalculate A^1,A^2,A^4,A^8 and A^16 . So if I need A^14 I have to do A^8*A^4*A^2 ,So where it has become O(n^2)??
Sir please explain both technique.
I will explain only the second technique. The first thing is just some non-asymptotic optimization, probably you don't need it to get AC.
You don't really need to find A14, you need to find A14v for some vector v. So you can represent it in the form A8(A4(A2v)). All multiplications are matrix-by-vector, they are O(n2).
Sir, At last I have solved it with 300+ line code.
Sir , What about the topcoder forums solution??
As far as I understand, solution from this forum also use matrix exponentiation, and matrix size is even more than in my solution, so I don't know how it can work fast without this trick.
Also you can read my code, it's much shorter than your. https://pastebin.com/8yeXvatX