I've been stuck on this problem for a while (Lazy Cows USACO 2005 US Open Gold) . I was able to get the recurrence correct . But my naive approach (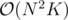 ) TLEs .
) TLEs .
First I compressed the positions by sorting them based on their column and breaking ties using the row number
Then I pre-processed 3 arrays
costH1[i][j] stores minimum area covered using a single horizontal rectangle , from ith smallest position to jth . If it's not possible (cows are not entirely up or entirely down) then its INF.
costH2[i][j] stores minimum area covered using 2 horizontal rectangles . If it can be covered with a single rectangle then its INF.
costV[i][j] stores minimum area covered using a single vertical rectangle . To be more precise , its a rectangle with top left coordinate at (1 , coordinate[i]) and bottom right at (2 , coordinate[j])
Using these 3 arrays
DP[i][j] stores the minimum area covered by i rectangles for a prefix area till jth column.
Base Case
DP[0][j] = INF
DP[1][j] = min(costV[0][j], costH1[0][j])
DP[i][0] = 0
My Submission : Commented Code
Can someone help me in optimising this recurrence relation.
Update
I would like to thank send_nodes for helping me in solving this problem .











Auto comment: topic has been updated by bhishma (previous revision, new revision, compare).
As j increases, what happens to the value for k which attains the minimum?
I feel that they should increase , because cost[k][j] ≤ cost[k][j + 1] for a particular k . Also DP[i - 1][k] + cost[k + 1][j] ≤ DP[i - 1][k] + cost[k + 1][j + 1] for 0 ≤ k < j , so the minimum index increases as j increases .
Yeah, so you can use divide and conquer opt. to solve it.
Sorry I'm not aware of divide and conquer optimisation . Can you please explain it briefly .
So first, you should do an outer loop on i, and an inner loop on j to compute the DP (using your variable naming above). Naive way is O(N^2), but D&C can do it in O(N log N).
Idea is that if you want to compute dp[i][x] for all x in a range [l,r], and you know that the possible values for k (again using your naming above) lie in the range [a,b], you should compute dp[i][(l+r)/2] first and note the k that attained this minimum, let it be p. Then, you can compute dp[i][x] for all x in range [l,(l+r)/2 -1] now using the k-range [a,p] and dp[i][x] for all x in range [(l+r)/2 + 1, r] using k-range [p,b]. It works because of that monotonicity condition.
There is a problem . Our assumption that k increases as j is wrong .
For this test case (TC 6)
Using the naive approach the k array looks like this
[-1, -1, 0, 2, 2, 1, 1, 6, 6, 8, 9, 8, 11, 11, 11 ...for i = 4.What should I do now ?
Oops, you're right. Look at my comment below.
In the second base case shouldn't it be: dp[1][j]=min(costV[0][j],costH1[0][j]) instead of i?
Thanks for the correction . I have updated it.
Auto comment: topic has been updated by bhishma (previous revision, new revision, compare).
Ok, I finally managed to get this problem accepted. I used a different dp state:
(index, number of rectangles left to place, is there a horizontal rectangle ending at (1,index), is there a horizontal rectangle ending at (2,index), is there a vertical rectangle ending at (1,index) and (2,index) ).
It has N*K*2*2*2 states. For transitions, to get to some state, you can extend the top rectangle, extend the bottom rectangle, extend top and bottom rectangle, extend a vertical rectangle, create a new top rectangle, create a new bottom rectangle, create a top and a bottom rectangle, create a vertical rectangle, discontinue a top rectangle, discontinue a bottom rectangle, disc. a top and bottom rectangle, disc. a vertical rectangle.
Time complexity was O(N*K*(2^3)^2) for my solution. Cool problem, thanks for sharing :D
What do you mean by discontinuing a rectangle .
at index i - 1 we had some rectangle (top, bottom, top&bottom, or vertical), and at index i, we don't put any rectangle in its place (we don't create a new rectangle nor do we continue it). I guess better word is "ending" a rectangle.
Thanks a lot I was able to solve the problem.
Auto comment: topic has been updated by bhishma (previous revision, new revision, compare).