The strict proof seems to be a little complicated as far as I consider, however an intuitive understanding suggests that the answer is n + n / 2, and it is accpeted...
We must find out all the intervals that consist of the same integers. For an interval with P integers, the number of reasonable subsequences is  . Thus, we can adopt two pointers to find out all the target intervals, and calculate the answer.
. Thus, we can adopt two pointers to find out all the target intervals, and calculate the answer.
As it has been guaranteed that no two circles intersect with each other, the given point can only fall into at most one particular circle (one special case is that two circles touch each other at the given point). Thus, we first sort the circles in an increasing order of their X-coordinates, and find out two circles between which the give point falls (check the X-coordinate of the given point as well, and a special case is that the given point falls at one of two ends of all the circles), which can be achieved by using binary search.
Then, the final step is to check which circle it falls inside, or completely outside all the circles.
The basic idea is still binary search. We use a[n] to denote the given array. We use binary search to find out the maximum T so that 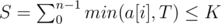 . Moreover, we compute K - S as the remainder. Then, any a[i] that is not larger than T should be firstly eliminated. Next we enumerate the first K - S survived a[j] in the natural order while decreasing them by one, and eliminate those a[i] ≤ T again. Finally, we start from the current position and output the survived indices one by one, by shifting to the right in a circular manner.
. Moreover, we compute K - S as the remainder. Then, any a[i] that is not larger than T should be firstly eliminated. Next we enumerate the first K - S survived a[j] in the natural order while decreasing them by one, and eliminate those a[i] ≤ T again. Finally, we start from the current position and output the survived indices one by one, by shifting to the right in a circular manner.
I spent about three hours modifying the algorithm to avoid the time limit....The most impressive modification I used is scaling the constant from 1 to  . This is the first time that I realized what an important role that a constant can play.
. This is the first time that I realized what an important role that a constant can play.
The general idea is to generate all the feasible patterns of maps and find out the one with the minimum distance and order. For instance, if letter 'a' and 'b' can be used, then we will obtain a map where we can move to positions of 'a' and 'b' while the other ones can not be used. With this equivalent map, we can implement BFS from the starting position until the terminating position is reached. During this process, we update the distance and also the minimum order if necessary.
As k can take values up to 4, we may have to check as many as C264 patterns for the worst case. It turns out that this will lead to TLE. Therefore, we have to further reduce the complexity. Instead of beginning from the starting position, we can begin from every one of the four positions that can be reached from the starting position. Each time we select one position, we have determined one letter that must be used and thus the number of feasible patterns is reduced to C253, which is supposed to satisfy the time limit as I consider.
However, I made a mistake that the number of generated patterns is in fact A253 rather than C253. As these two values only differ by a constant of  , I did not realize (or believe) that such a constant matters so much. After I correct the mistake, it passed... What a fascinating problem!!
, I did not realize (or believe) that such a constant matters so much. After I correct the mistake, it passed... What a fascinating problem!!










Can you please explain 84D?
Yes, of course.
Let us first focus on the meaning of finding out the maximum T so that . In fact for the i-th animal, under some T, the value of min(a[i], T) indicates how many times this animal can "contribute to the doctor". For an intuitive understanding, suppose that a = (2, 3, 4, 7, 6) and K = 18. Then, according to the above formula, we have T = 4. This means that the doctor will visit the 1st animal for 2 times, the 2nd animal for 3 times, the 3rd animal for 4 times, the 4th animal for 4 times, and the 5th animal for 4 times, which gives totally 2+3+4+4+4=17. If we set T to be some larger value, this makes no sense since the doctor can only have K = 18 times to visit animals.
. In fact for the i-th animal, under some T, the value of min(a[i], T) indicates how many times this animal can "contribute to the doctor". For an intuitive understanding, suppose that a = (2, 3, 4, 7, 6) and K = 18. Then, according to the above formula, we have T = 4. This means that the doctor will visit the 1st animal for 2 times, the 2nd animal for 3 times, the 3rd animal for 4 times, the 4th animal for 4 times, and the 5th animal for 4 times, which gives totally 2+3+4+4+4=17. If we set T to be some larger value, this makes no sense since the doctor can only have K = 18 times to visit animals.
Next, after finding out the maximum T, we can see that the remainder K - S ≤ N always holds. The reason is that if K - S > N, it means that we can further increase T to T + 1 while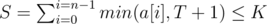 still holds (but we have assumed that T is the "maximum" one, which is contradictory). The formula of K - S ≤ N is very important since this implies that we can simply simulate for the remaining K - S times to see which animals are still in the queue. We can just enumerate the remaining animals one by one (use a "for" loop) and decrease the corresponding a[i] by one until all the K - S times have been "visited" or there exists no a[i] > 0. Finally, we start from the last animal (this one will stand in the front of the queue) when we exit from the "loop", and output the survived animals one by one, like a circular array.
still holds (but we have assumed that T is the "maximum" one, which is contradictory). The formula of K - S ≤ N is very important since this implies that we can simply simulate for the remaining K - S times to see which animals are still in the queue. We can just enumerate the remaining animals one by one (use a "for" loop) and decrease the corresponding a[i] by one until all the K - S times have been "visited" or there exists no a[i] > 0. Finally, we start from the last animal (this one will stand in the front of the queue) when we exit from the "loop", and output the survived animals one by one, like a circular array.
The trick of this idea is that instead of simulating step by step, we try to find out the "most border", and start simulating from there.