Let's denote the potion's amount of experience as exp and its cost as cost. We want to know if there is a potion such that exp and cost meet the following condition: 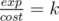 . To do this, we can iterate on cost from x to y and check that exp = k·cost is not less than l and not greater than r.
. To do this, we can iterate on cost from x to y and check that exp = k·cost is not less than l and not greater than r.
To understand whether some piece of sausage intersects with pizza, we can check if their borders intersect. And to check this, since their borders are circles, we are interested in their radii and the distance between their centers.
To check if a piece of sausage is inside the crust, we firstly check that it is inside the pizza 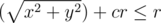 ), and secondly check that it is completely outside the central part of the pizza
), and secondly check that it is completely outside the central part of the pizza 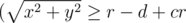 ).
).
It's easy to see that if the number written on some vertex i is not equal to 0, then its beauty will be some divisor of ai. Also if the number written on the root is 0 then the beauty of each vertex can be easily calculated. Otherwise beauty of each vertex will be a divisor of the number in the root.
Let's calculate the beauty of each vertex if the number in the root is 0. This can be done by traversing the tree, and the beauty of i is gcd(ai, ans[pari]).
If the number in the root is not 0, then possible values of beauty for each vertex are among divisors of this number. For each of these divisors we can maintain how many numbers on the path from the root to current vertex are divisible by that divisor. When we enter or leave some vertex, we need to update this information by iterating on divisors of the number in the root. If we maintain it and current depth d, then we can calculate the possible beauty of current vertex. It is equal to greatest divisor such that there are at least d - 1 numbers on the path that are divisible by this divisor.
842D - Vitya and Strange Lesson)
If the last query was xi and then we receive a query xi + 1, then we can leave the original array unchanged and use the number 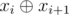 as the second query. So we will maintain current xor of queries instead of changing the array.
as the second query. So we will maintain current xor of queries instead of changing the array.
It's easy to see that if the array contains all numbers from zero to 2k - 1 and the number in the query is less than 2k, then the array will still contain all those numbers.
Let's store all numbers from the array in binary trie and maintain the number of leaves in each subtree.
To answer each query, we will descend the trie. We need to get the lowest possible answer, so if current bit of the number in the query equals i (i = 0 or i = 1), so we firstly check the subtree that corresponds to bit i. We will descend into the vertex only if the subtree is not a complete binary tree (so there exists a number that would belong to this subtree but is not included in the array). When we try to descend into an empty subtree, then we set all remaining bits in the answer to zero.
The vertices in the answer are the endpoints of some diameter of the tree.
Let's consider diameter (a, b), where a and b are its endpoints, and we add a new vertex с. Then the length of diameter either remains the same or increases by one (then new endpoints are vertices (a, c) or (b, c)).
We have to maintain current centers of the tree (there are not more than two centers). If the length of diameter increases, then the number of centers changes (but there will always exist a vertex that was the center before the query and remains the center after the query).
Let's build a segment tree on the eulerian tour of the tree. The vertex that maintains the segment [l, r] will store current maximal distance to the center and the number of vertices that have this distance. Then the answer for the query will be stored in the root of the segment tree.
When we add a new vertex, we need to check whether the length of diameter increases; this can be done with LCA. If the diameter increases, we update centers and distances to them.











Solutions to the problems are not accesible.
Thanks, i change it
I think problem C, we don't need to consider the first case which root's value equal 0. Doing the latter is enough.
Can you please have a look at my code and point out what's going wrong? TIA. My Code
In problem C, in the sample code, I dont understand this line.
Should it not be ...
Since, its enough to have only d-1 divisors from the root to that node in that path, why should we check dist, when dist-1 itself satisfies the condition? Could someone help me out with this?
dfs2(0, 0);
Oh yes, missed that! Thanks a ton!
"Let's build a segment tree on the eulerian tour of the tree." <3 <3 <3
I did not understand the solution for the D question. Could someone please explain the solution?
I will explain my solution, I hope it helps you. I must say that my implementation is not the most elegant and efficient one (for example, I could have used an array instead of pointers).
29914047
We must take into account that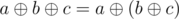 (
( means a xor b). This property allows us to consider the original array xor some number instead of the original array xor the first query xor the second query... That is, we can accumulate the xor of all the queries and do the xor with the original array with this value.
means a xor b). This property allows us to consider the original array xor some number instead of the original array xor the first query xor the second query... That is, we can accumulate the xor of all the queries and do the xor with the original array with this value.
Also, we must note another thing: the mex of an array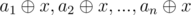 will be a number
will be a number 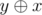 such that y is not present in the original array a1, a2, ...an. Why? because the xor operation fulfills the following property:
such that y is not present in the original array a1, a2, ...an. Why? because the xor operation fulfills the following property: 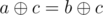 if and only if a = b. That is, any value that is not some
if and only if a = b. That is, any value that is not some 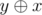 will surely be equal to some
will surely be equal to some  such that z is present in the original array. So now our problem is about finding the minimum value
such that z is present in the original array. So now our problem is about finding the minimum value 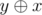 such that y belongs to a fixed set of numbers (the ones that do not appear in the original array in a given interval).
such that y belongs to a fixed set of numbers (the ones that do not appear in the original array in a given interval).
With this knowledge we can build a Trie (https://en.wikipedia.org/wiki/Trie) with the numbers that do not appear in the original array between 0 and 220. We can build it as follows: starting from the 20th bit, use the bit values to decide if we go to the left or to the right.
Assuming we are going to the right when our bit value is equal to zero, we can see that we can retrieve the smallest value stored in our trie by simply going to the right whenever it is possible. We can retrieve the minimum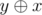 by traversing the Trie as follows: for each level i we will take into account the value of the ith bit of the current query value. If the current bit is equal to one then we must observe that all the ith bits in our set of valid numbers will have their values flipped, so we should also flip the meaning of the edges of the current node.
by traversing the Trie as follows: for each level i we will take into account the value of the ith bit of the current query value. If the current bit is equal to one then we must observe that all the ith bits in our set of valid numbers will have their values flipped, so we should also flip the meaning of the edges of the current node.
Thank you so much! It was a very clear and easy to understand explanation.
Hi! Could you please help me to understand, why the first submission gets ACC, while the second one gets WA?
The only difference between them is that in the first submission I consider range [0, 2^20-1] (as you do) and in the second I consider [0, 300500] (because all numbers & queries don't exceed 3*10^5)
We can manage to create a number that exceeds 300500 by xoring two numbers between 0 and 300000. For example: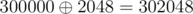 .
.
Why? Because 300000 = 10010010011111000002. The 11th bit is not set and 211 = 2048, which is smaller than 300000, however, 300000 + 2048 = 302048.
In problem C div 2 , i tried dfs(int node , int max , int simple_gcd) , here max is the maximum beauty possible of parent node if we have already set 0 on an ancestor node and simple_gcd is gcd of all numbers excluding the node we are on .....
At each node i can either make the current node 0 (in this case the gcd will be previous/parent node) or let 0 be in previous optimal position ( take gcd of max with current node a[n] )...
For example if we had a 5-->10-->7-->15 (1-->2-->3-->3-->4) , we would maintain two variables max and simple_gcd at each step initially, for the root node ans[1] = a[1] = 5 , and for 1st node under root , i.e 10 ans[i] becomes max(a[root], a[node]) which means we make minimum element 0 , now dfs starts to find ans of all nodes below, for node 3 we have max = 10 (0 is set at 1st node(5) ) and simple_gcd = 5 (no zero set uptill now therefore simply the gcd uptill here) , now i compare max of (simple_gcd , gcd(max , a[3]) ) which gives me ans[3] = 5 , and i keep moving on this way...
Currently i am getting WA on test case 4...anyone has any suggestions ?? Here's my submission http://codeforces.com/contest/842/submission/29929743
It's my favourite solution, so look you don't need to take max nod everytime. The test is something like 4 6 2 3 2 1 2 2 3 3 4
Actually it looks like this solution is a bit different than the one you have described , but i don't get where my solution is being wrong.... could you by any chance give test case 4 as majority of the people seem to be getting it wrong. Btw my code pAsses the test case you have given...
4 6 2 3 2 1 2 2 3 3 4 It' s not test, but it also a hack look problem is you take 3 and can 2, so when you meet 2, you write 1 and the answer is 2
4 6 2 3 2 1 2 1 3 3 4
your solution print 6 6 6 2
But answer should be 6 6 6 3
In problem A it is said that efficiency may be a non-integer number, but in editorial we think that it is integer and don't check if exp = k*cost is non-integer
Look, in input of problem A is said K IS INTEGER, but when we count k = exp/cost, k can be noninteger
Help me, please!
I'm trying to solve problem C, but I believe I will face the same problem as in problem C / Div.2 (Codeforces Round #428).
Tell me, please, why my solution is too slow? Here is my programm: http://codeforces.com/contest/839/submission/29901357.
In Problem C tc1 shouldn't the answer be 6 2 , bacause in 1 gcd is 6 , but in 2 gcd is gcd(ans[1],a[2]) that means gcd(6,2) which is 2..
No, shouldn't. "For each vertex the answer must be considered independently". ______________________________________________________________
So, let's calculate the beauty of the vertix 2.
1) We can change the number in vertix 2 to 0, then the answer for the vertix 2 will be gcd(6, 0) = 6.
2) We can change the number in vertix 1 to 0, then the answer for the vertix 2 will be gcd(0, 2) = 2.
3) We can leave all vertixes unchanged, then the answer for the vertix 2 will be gcd(6, 2) = 2. __________________________________________________________
So, the beauty of the vertix 2 is max(6, 2, 2) = 6.
thanks brother
As you can see, this formula "ans[i] = gcd(a[i], ans[par[i]])" is used if the nubmer in vertix 1 is 0. In this case the answer for the vertix 2 is 2.
But there is the other case, when the number in vertix 1 isn't 0. In this case the answer for the vertix 2 is 6.
So, the beauty of the vertix 2 is max(2, 6) = 6.
I noticed that problem E is also labelled with the "binary search" and "divide and conquer" tags, may someone share how to solve the problem in this alternative approach? :)
Perhaps this may help?
We can use this fact — if some vertex isnt some diameter border after some step, she isnt diameter border after next steps. Now we can count any diameters after all steps and use binary search for all vertexes so that find the first moment, when every vertex already not diameter border. Sorry for my English :)
Many thanks to both of you, now I understand how to solve it in this way. :]
Can problem C be solved like this?
Let f(u, x) is the maximum beauty for node u and we have chosen x parent nodes (0 <= x <= 1) to change their value to 0 (because only the value of ancestor vertices affect the beauty of node u) . Then we have this formula:
Let p be the parent of u.
f(u, 0) = gcd(f(p, 0), a[u]).
f(u, 1) = max(f(p, 0), gcd(f(p, 1), a[u])).
Then for each node u the answer will be max(f(u, 0), f(u, 1)).
I haven't tested this solution, but I wondered will this solution work? (correct me if I'm wrong)
It doesn't work in this case: (take the path as an array)
[9, 6, 4, 2]
f(4, 0) = 1, f(4, 1) = 3 f(2, 0) = 1, f(2, 1) = 2 which has nothing to do with f(4, 1) or f(4, 0)
why is it failing? haleyk100198 looks like a pretty brute force approach.
The question can not be solved by greedy since you may have to switch prime factors as the list gets longer. As you can see the list [9,6,4] originally has only 1 element that does not have 3 as a prime factor, and same applies to 2, but since 3 > 2 the greedy approach is taking 3 and discarding 2 as a possible solution. When [2] is appended to the list and we must discard 3, this approach fails to recognize that we can fall back to 2.
I coded same thing on contest and realised it was not correct. You can check my submission of profile. I think its same logic as yours, so check it if you want.
for problem E:
this is a quite simple code! http://codeforces.com/contest/842/submission/29919946
But I can not understand why this is correct,who can help me :(
Now I see. You maintain the ends of diameters. When You find new longer diameter you just update sets. It's fast because you can change set for vertex x only when it was a new end of bigger diameter.
Yeah,you're right
The point is the length of every path with one endpoint in s1 and another one in s2 is the same.Then we could just calculate one time to get the length of path with endpoint v
Thanks for your reply
I have a question about this solution. For a tree like: 1-2 2-3 3-4 4-5 3-6 6-7 6-8 Is it possible that s1 = {5, 7, 8}, s2 = {1}, and then add 8-9,getdis(9, 5) is larger, then s1 = {1, 5, 7, 8}, s2 = {9}?(7,8 should not be in the set) I just want to describe how the tree and the set look like(my English is quite poor, sorry), in fact, s1 = {1}, s2 = {5, 7, 8}, after the edge 8-9 is added, s1 = {1, 5}, s2 = {9}
Thank you for your reply! But what if a, b, c have the same length with other node? And I can't understand why s1 is an one-element set. s1 and s2 always choose the smallest node to get the distance, is this feature ensures the correctness?
Oh,I think your tree will get two sets as these: s1={1},s2={5,7,8} before the addition of edge (8,9) You see,the code initially set the s1 as {1},when the diameter update by the new edge,for example,firstly it always add an edge such as (1,2) because there is only vertex 1 in the tree now,so after this addition there will be s1={1},s2={2}.
Back to your tree,1-2 2-3 3-4 4-5 3-6 6-7 6-8,it certainly will get s1={1},s2={5,7,8},because the code initially set the s1 as {1},as the code also maintains these two sets as these tricks:when add a new vertex it will compare the two distance to the two sets which are the endpoints of the diameter last time.If the distance between the added vertex to the s1 elements are longer than the diameter before,then is time to update the diameter and change the two sets(You'd better draw a simple picture...):for each element in s2,if one can also form a diameter with the added vertex,then this element will be add into s1 because the new endpoints are the new added vertex and all the vertexes which are in the tree before and form the new diameter as well.Then the added vertex became the other endpoint(in this case,s2).
When the distance between the added vertex to the s2 elements are longer than the diameter before,it's similar to this.
And the situation when new added vertex can not exceed the old diameter but can be a endpoint is like max(dis1,dis2)==mx in the code.Then you simply added it into the correct set is good.
So s1 and s2 is not always choose the smallest node to get the distance,and certainly is not the feature ensure the correctness(As you mentioned)
p.s. Sorry for my bad English and bad description
For Div.2 C. Why the editorial solution guarantee that result will be max? I don't get it.
Let's consider that there is a better solution for current vertex. If the value in the root is not 0 the answer for current vertex is one of the root's divisors, but following the editorial we have already taken max root's divisor which occurs at least (depth — 1) times. So, there is not a divisor bigger than that. We got a contradiction => the tutorial's solution is right.
For Problem A — Kirill And The Game — it may be very time-consuming to iterate on cost from (x) to (y), or to iterate on experience from (l) to (r), when ( y — x ) or ( r — l ) is a very large number, as all these numbers range between 1 and 10,000,000.
A much more efficient loop-free approach is to compute the intersection of the two intervals:
expressed as: min_experience <= experience <= max_experience, where min_experience = max( l, k . x ) and max_experience = min( r, k . y ).
The answer to the problem instance is "YES" if the experience-interval intersection is not empty and contains at least one multiple of k; otherwise the answer is "NO".
In order to not iterate through the intersection interval, it is sufficient to compute the corresponding cost interval: min_cost <= cost <= max_cost, where min_cost = min_experience div k and max_cost = max_experience div k.
The answer to the problem is "YES" if ( min_cost < max_cost ) or ( min_cost = max_cost and min_experience mod k = 0 ); otherwise the answer is "NO".
The following is a C++14 implementation of this algorithm.
http://codeforces.com/contest/842/submission/29941778
Just for curiosity, there is some way of do the A in O(1)?
Here, you just check if there is any valid answer by merging two intervals
http://codeforces.com/contest/842/submission/29946062
Glebodin In problem C , you are considering only root to be 0 and comparing it with dfs2 results, but when calculating beauty of other vertices, other than root vertex can also be zero. Also why did you write
at the end of dfs2() ? ans[] in upper recursion calls are already calculatd. we are not using koll[] in upper recursion calls. then why update it?
1) we look not only root 2) because we count something in son and need to clear it Maybe i misunderstood i
apologies, I misread the question.I see we are also considering other nodes to be zero. and yes we need to clear the count that we calculated in a son so that other sons can use the original count that their parent had passed. Thanks, It is clear now.
Nice to help you
Can someone please tell why my code is getting WA at test 14? Link Thanks in Advance!
change 300500 to 600500 and it's AC
For Div2 C, if 0 would be an allowed value for a[i], (and hence root's value could be 0 initially) then how would one go about solving the problem?
For problem E : Can someone explain to me what "diameter of the tree" is, please ? Sorry for my bad English .
it seems like the max length of the two vertexes in the tree.
Thank you so much, I am very happy to receive your comment. Now, I know what "diameter of the tree" is. Could you explain to me more clearly about problem E , please ? =)))
Sorry for my bad English =)))
Yes,it is the max length of the two vertexes in the tree,you can get it by dfs two times.
Thank you for replying my comment !!! =))) Sory for my bad English =))
Can Div. 2 C be solved like this?
I am maintaining 3 arrays. Their definition is like this:
total[i]holds the gcd of all number on the path from root to node i.zero[i]holds the beauty value if we put 0 in the node i.not_zero[i]holds the beauty value if we don't put 0 in the node i.Then lets have a function that gives me the beauty value named
beauty(_node,par)that gives me the beauty value of_nodewhich has parent namedpar.If I put 0 in current node, then I couldn't put any 0 in any of the previous node on the path from the root.
If I don't put 0 in current node, then I could put a zero in any of the nodes that are on the path before this node.
Then the answer for each node is
max(total[_node],max(zero[_node],no_zero[_node]))But this solution gives WA on test case 7. Can anyone give a small test case for which this solution is wrong?