Hi, everyone!
On September 10, 2017 at 13:00 Moscow time the final round of Russian Code Cup 2017 will take place! The round will be 3 hours long. 55 participants of the final round will compete for prizes and glory, and we are eager to watch their competition at http://russiancodecup.ru.
And we have a nice surprise for the others: if you would like to apply your skills at our finals problems, come to codeforces.com after the Finals is over, at 16:35 Moscow time, the round featuring RCC Finals 2017 problems will take place, open for everybody.
Some notes:
- Round will use ACM rules;
- It will be unrated;
- Problem difficulty will be close to Div 1 round;
- We ask RCC finalists not to publish or discuss problems after the end of the Finals before the CF round ends, of course you shouldn't participate in CF round;
- Judging machines at RCC and CF are different, "my solution passed/failed at CF, and it was different at RCC" is not a valid appeal.
UPD The official contest is over, congratulations to the winners! And good luck to CF Round participants.
UPD2 Editorial












The online mirror probably coincides with TCO17 Wildcard Round, right?
According to this calendar TCO17 Wildcard and also rated "Fun SRM" is held in 19:00 MSK to 22:00 MSK, and RCC online mirror is held in 16:35 MSK to 19:35 MSK.
The title says “Teams Allowed”. But how can I register as a team member?
rated or unrated ?
Funrated.
For me! It is Downrated!
You are completely right because that t.me/ContestWatcherBot has just sent me "ContestWatcherBot: System testing has finished for Russian Code Cup 2017 — Finals Unofficial Mirror, Div. 1 Only Recommended, Teams Allowed. Waiting for rating changes." Actually,I have afraid of it because I couldn't solve any problem so I will take downrated by FUNRATED (cheating)
It's fixed, and the calendary says unrated also.
I think rated->unrated is very gaoxiao.do you think so?
.
Round is unrated, BUT you could find possible rating change here (after round starts)
Extensions for browsers:
Have fun
& high rating:)Are you first time hear about CF-Predictor? You could read about it in my blog
======================================================================
Раунд не рейтинговый, НО посмотреть возможное изменение рейтинга можно тут (после начала раунда)
Расширения для браузеров:
Удачи
и высокого рейтинга:)Впервые слышите про CF-Predictor? Можете прочитать про него мой блог
Additionally to the official standings, there are contestant list, standings with TC and CF nicknames, text translation of contest flow on English and on Russian available.
rip judge
What does Judgment Failed means ??
I answered the first problem then i submitted it then i get (Judgement Failed) what does this mean
Judgement Failed??
So will it be fixed?
I don't know. :(
Now I understood why it was recommeded for Div 1 round! Because of its Statement
Was E maximum interval tree?
I think I have a solution based on that idea, but it got TLE despite being N log N. I think my function to determine whether the intersection point is inside the circle is too slow (right after the contest I realised a much simpler way to test it, but during the contest I had to use a bignum class to avoid overflows).
I used a bit different idea. Every satelite covers the area, but also the arc of the circle. So i made interval tree for the arc coverage and checked if min(i, j intersection) <=2. It got TLE :(
I solved E in a robust way, maintaining points with (angle OAP, angle OBP) The common covered area by (A, B) and (C, D) is (min(A, C), min(B, D)). To cope with query 3, I checked if all points other than i, j don't have (P, Q) such that P >= min(A, C) and Q >= min(B, D) and the point is not in the circle. This can be done with ordinary segment trees.
I sort the points by angle made at A and at B, and rank them. Then I place them in a new coordinate system, where x1 < x2 means A-P1-P2 is counter-clockwise and y1 < y2 means B-P1-P2 is clockwise. Now satellites P1 and P2 can be connected if there is an intersection outside the planet, and there is no other satellite (x, y) such that x <= max(x1, x2) and y <= max(y1, y2) in this other coordinate system. That I do by keeping the smallest y coordinates for each x coordinate (using a set for each x coordinate), and then maintaining a segment tree over those.
The intersection of two satellite coverage area can be formed as a satellite-like coverage area.
If this satellite-like coverage area is covered by other satellites, there will exists at least one satellite coverage area which contains this satellite-like coverage area (instead of some union).
Considering the projections of coverage areas on the half-circle border (as intervals), the query is equal to determine whether there exists one interval (except i-th and j-th) which is able to cover the intersection of i-th interval and j-th interval.
When I finally realized that, I tried to modify my wrong solution but actually I didn't have enough time :(
Our recommended solution is to sort all the intervals by their left endpoints, and use a segment tree to maintain the maximum right endpoints, which can be done in .
.
How to solve B? Is it some kind of greedy? (Just a wild guess since it looked NP-complete)
Yes, greedy by decreasing of length.
If we sort all prefixes by decreasing of length, we can take them greedy. And with hashes we can check if we can pick current prefix.
why & how would the sorting work ? could you please explain ?
Let's look at the longest string at the moment. If we will take it to the answer, we block only one string — the taken one without first letter, and because from these two strings we can take only one, our move is not worse, than any else. Thus, if at each step we take the longest possible string, then we get the best answer.
Thanks a lot . :)
I tried something different. I'm pretty sure my idea is valid but my implementation is wrong. This is my idea: first of all, we will use rolling hashing to quickly compare strings. We say string A is a child of string B if the first letter of A can be removed to get B. We construct a tree or many trees with all the prefixes. Now the problem is equivalent to the most nodes you can "color" so that no two adjacent nodes are both "colored". You can solve with two dp arrays. dp1[i] will be the most you can color in the subtree of i while coloring i. dp2[i] will be the most you can color in the subtree of i without coloring i. We get the recursive formula that dp1[i] = 1 + sum of dp2 of children and dp2[i] = sum of max(dp1, dp2) of children.
build the trie
build another graph G where the vertices are the nodes of the trie (all possible preffixes) and add an edge from v to u if string v can be obtained from u by removing the first letter
G is a forest
now the problem can be solved with dp
I thought exactly the same till step 3,and couldn't do more, can you explain step 4 (dp).
maximum independent set in trees, f[u][b]=maximum number of vertices we can take from subtree u, b can be 0 or 1 indicating if we can pick or not u
I solved with DP, but there was people that solved in 11 minutes, maybe there is an easier solution. My idea, lets consider every prefix of all strings and build an graph, where exists an edge between the prefix and the prefix without the first letter. It will be a forest. No two adjacent vertex can be at the set and just the vertexes that are prefix can be choose. Since you have to find maximun, you can apply dp.
Am I the only one who used Aho-Corasick for B? Using suffix links, we can build a forest and the problem reduces to finding maximum independent set in a forest, which is straightforward.
I don't think Aho-Corasick is exactly what you need: you want to link each node to the suffix formed by removing exactly the first character (or no link, if no such node exists), whereas Aho-Corasick will link to the longest suffix that does exist.
Yes, it's an overkill but I can add a check if the longest suffix is obtained by removing exactly 1 character.
@flashmt: No
@bmerry: Easy enough to add the "only one level up" check :)
What was the solution idea for problem B ?
How to solve A??
Observe the input. check the difference between any 2 numbers in given array. B should not have this difference. Choose smallest number which is not one of these differences as b[1]. Repeat from b[2] and so on
but it is not correct for this test case i guess...
2 1 4
as diff is 3 we can take b[1]=1 b[2]=4 as u r saying....
.| 1 4
1| 2 5
5| 6 9
It's always possible — just greedily add the smallest possible element to B that doesn't violate the constraints.
How to solve D?
centroid decomposition and dp f[u][v]=maximum beauty of subtree u if vertices in the path u->v are in a cycle
What are u, v in this case? I assume it can't be all vertices in the tree, since that would be O(n^2).
when doing centroid decomposition the sum of sizes of roots is nlogn
I've started implementing a solution using centroid decomposition and think I understand where u and v come in: they're one of the paths, clipped to the current tree — hence either u or v is the exit to some ancestor root, which constrains the search space.
However, I've still having some trouble. Let's say I have a tree rooted at r with two subtrees S and T, and I want to compute f[u][v] for some u, v both located in S. I then compute f[u][v] within S and I compute the maximum beauty in T. But then I also need to consider adding new edges whose paths pass through r (from S to T). This means I now need to consider two constraints in S: u->v must be untouched, but so must the part of the new path that lies within S.
Any tips? I've not used centroid decomposition much so I may be missing something standard.
Maybe a DP on the tree, using some data-struct like segment tree to obtain the sum of a path. The answer of the subtree of node x is ans[x] = max(sans[x]. max{i.c + sans[x] + sum(x,i.a) + sum(x,i.b)}), for i in V[x], V[x] is the set of input triple<a,b,c> where lca(a,b)=x, sans[x] = the sum ans of x's children, sum(a,b) if the sum of value[x] for each x on the path(a,b), value[x] = sans[x] — ans[x]
dp[v][0] — maximum beauty of substree when v is not in any cycle
dp[v][1] — maximum beauty of substree when v is in cycle
We have u, v, cost. Let's try to add cycle at lca(u, v). In order to get right sum we need to count on path from u, v to lca the sum of beauties not including this path. It can be done by calculating sparse table the same way we do with lca. O(nlogn)
let dpnode be the maximum sum of edges you can add such that those edges belong in this subtree and the subtree is still a cactus.
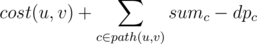 .
.
let
Then if you do not make any cycle pass though node then dpnode = sumnode. otherwise if you take the edge (u, v) , lca(u, v) = node and make it's cycle pass through node , then dpnode is
All you need to do is tree sum updates and queries which can be done by building a bit on dfs start end times easily in NlogN.
Where can I resubmit my code of this contest? emm... I think I will get AC this time.
How to solve A?
Brute force, since all b[i] <= 1e6, you can try for each i in {1..1000000} to loop through the array a and find for each a[j], if i+a[j] is visited before, if not add that i to the answer list, and mark i+a[j] for all a[j] as visited, you need to break when the answer list equal to n.
Five years ago I wrote C.
How to solve F? It looked like the most interesting problem.
Can option to upsolve problems on CF be enabled?
Can't submit solution now. When will be it in archive ?
Please enable upsolving.
why unrated....