96A - Футбол

Count the maximum length of repeated elements, and compare it with 7.

96B - Счастливые числа (упрощенная версия) 95B - Счастливые числа

We store the integer as a string and use L to denote its length. At first, note that if L is an odd number, the answer should be 44...477...7 with 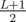4s and 7s. If L is an even number, we can first compare it with 77...744...4. If the former one is larger, the answer must be 44...477...7 but here both the number of 4 s and 7 s are 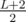; otherwise, it implies that we can always find a required integer with the same length L.

This minimum answer can be found by using DFS (it seems that DFS is an incredibly powerful technique...). The DFS works as follows.

We use s[pos] to denote the digit that we are dealing with at position pos, and use num4 and num7 to denote the number of 4s and 7s that are still not assigned. Initially, .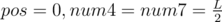

At first, if num4 > 0, we try to assign 4. If s[pos] < '4', it is obvious that we can safely assign 4 and the final answer is thus straightforward. If s[pos] =  = '4', then we should call DFS again to deal with position pos + 1 with num4 = num4 - 1. If s[pos] = '5', or'6', then we assign 7, and the answer has been determined. If s[pos] =  = '7', then we call DFS to deal with pos + 1 with num7 = num7 - 1. If s[pos] > '7', we should return 'false'.

96C - Хоккей

As the strings have small length, we can adopt exhaustive search to find all the positions that should be replaced. We use T to denote the given letter. For each position, if it is not equal to T, we should replace it with T in order to achieve the maximum number of T; otherwise we should further check whether T is 'a' or not. If yes, then we replace it with 'b', and if no, we replace it with 'a'. Be careful that the lower case or upper case should stay the same.

96E - Конные скачки

This is a sparse graph, and thus we can implement Dijkstra algorithm based on priority queue with complexity O(ElogE), where E is the number of edges.

With the above arguments, we can implement Dijkstra to every node, and find out all the nodes that it can reach. Then, we can build another new graph with the given cost, and it is sufficient to implement Dijkstra algorithm again to find out the shortest distance between the given starting point and ending point.

95E - Счастливая страна

It turns out that this problem has a standard solution. At first, we adopt Union-Find technique to calculate the number of components and also the corresponding sizes. Then, the problem is reduced to a well-known, perhaps referred to as "Multiple-Pack" problem, and one can search a lot of information on the Internet.