We can adopt a triple loop to enumerate all the reasonable combination, and find out the one with the minimum cost.
A simple implementation problem. Keep adding all the digits to obtain a new integer, and repeat again until it is reduced to an integer with only one digit.
At first, we count the number that each letter has appeared in the string. To eliminate the number of different letters as many as possible, it is straightforward to first delete the letter with the minimum number, and then the one with the second minimum number, and then the one with the third minimum number, and so on.
Although n can be as large as 109, the value of m in fact has determined that at most 2m of the nodes (stops) really affect the result, since the person can only get off the bus at these specified stops.
Thus, we should first compress the number of nodes (or stops) to the order of O(m), which can be achieved by using 'map' of STL in C++. Now we use dp1[k] to denote the number of different ways to get to node k. Furthermore, we maintain a prefix-sum array dp2[k] which have values 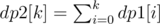 . For a route from node i to node j, we can calculate
. For a route from node i to node j, we can calculate 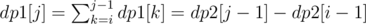 . Therefore, to compute any dp1[k], we should find all the routes that can reach node k, and add them together as shown above. Besides, the calculation of dp1[k] should be implemented in an increasing order of k, and do not forget updating dp2[k] = dp2[k - 1] + dp1[k].
. Therefore, to compute any dp1[k], we should find all the routes that can reach node k, and add them together as shown above. Besides, the calculation of dp1[k] should be implemented in an increasing order of k, and do not forget updating dp2[k] = dp2[k - 1] + dp1[k].
It is convenient to denote a point P with coordinate (x, y) as P = x + iy, where the complex form is introduced. Suppose that we have implemented several operations, and whatever the order of the two given operations are, they can always be described as repeating the following steps cyclically: first add vector C to vector A for m times, and then rotate the resulted vector for k times (both m and k can have zero values).
Thus, after the first cycle, A becomes (A + m1C)ik1 = Aik1 + m1Cik1. After the second cycle, it turns out to be Aik1 + k2 + m1Cik1 + k2 + m2Cik2. Note that ik can only have a form of i or 1. Thus, after several cycles, the resulted vector must have a form of Aik + aC + biC, which should be equal to B. This equation is satisfied if and only if both real and image parts are equal, respectively.
Look out for the case where C is a zero vector.
The main solution consists of two steps.
Step 1. Implement DFS from the root node 1, and during this process, we should compute several variables.
childnode[n]: the number of child nodes that node n has;
total_t[n]: the time consumed to visit all the child nodes of node n while finally returning back to node n;
Step 2. Implement BFS to calculate the required answer. However the order of visiting next nodes should be carefully optimized, which is more complicated than I thought... One can check the tutorials in http://codeforces.com/blog/entry/2393, and the necessary variables to determine the visiting order has been obtained in the DFS step.









