
Can this be done in O(n^2) space and O(n^3) time? Please share your approach.
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |

Can this be done in O(n^2) space and O(n^3) time? Please share your approach.
| Name |
|---|



Auto comment: topic has been updated by ankeshgupta007 (previous revision, new revision, compare).
First, you need to sort the values in non-decreasing order.
In this question, first of all, to think of a solution that will require O(n^3) space and O(n^4) time is actually pretty easy.
The States would be i,j,k where dp[i][j][k] would represent the min value of arranging the numbers from index i to j in a BST such that the root node is at a depth k. Now to calculate the value of dp[i][j][k] we will iterate from index i to j and consider one by one each index as the root. We can easily think of the recurrence for this. So I am assuming you already know that part.
Now in the above approach, we are keeping the depth also as a state. To reduce the complexity by a factor of n we can avoid keeping depth as a state. I will roughly explain my approach the main idea is if you have the value wi * (hi ^ 2) for any index i, when you will increase the depth by 1 the new value would be something like this wi * ((hi + 1)^2) which can be derived from the previous value directly. All you need is some extra values while calculating the new values,
wi * ((hi + 1)^2) = wi*(hi^2 + 1 + 2*hi)
which is wi*(hi^2) + wi + 2*wi*hi.
So the extra values which we need to store is summation of wi and summation of wi*hi. And you can get the new value which is wi * ((hi + 1)^2). And its also easy to get the new value of wi*(hi + 1). Because that would be wi*hi + wi and both the values are already there.
PS: I know I have not provided a good explanation but I think if you have the idea of the straight forward dp of this question you will get the idea of optimization from my explanation.
I understand your approach. But what is doubtful is that, when I am updating my DP tables, I am optimizing wi*(hi^2) rather than wi*(hi^2)+2*wi*hi +wi.
What I am trying to clarify is that are we making any implicit assumption that minimizing wi*(hi^2) simultaneously minimizes wi*(hi^2)+2*wi*hi +wi (because thats the term that is included in further calculations)
PS: Sorry if I am thinking something wrong.
Here is the code, I have not added memoization. It's just the recursion part. I got your doubt actually you need to look at the fact that we want to optimize only wi*(hi^2), the other values need not be optimized. We only want the other values to calculate the new values of the given function. I haven't tested my code on any test case, so do point out if you find any mistake in the implementation.
Implementation isn't a problem. Problem is when you calculate all 3 DP table for range {i,...,j} , and use the same for k=j+1 in range {i,...,j,j+1,..}, you actually include wi*(hi^2)+2*wi*hi +wi and not wi*(hi^2). Thats where the subtlety lies.
Oh okay, I got the mistake. My approach is incorrect. Sorry, for suggesting you wrong approach.
Could you find a test case for the same?
I think that it might just hold true in this case, just a possibility.
I tried many small random cases but the solution is giving correct answer actually. I am also surprised to see that the solution is working. Actually, the above code without memoization is surely correct but I thought when we would apply memoization then it would become incorrect because of the same reason you provided above. Currently, I am also not completely satisfied regarding why the solution is working. So, if you get the intuition behind the correctness please do share.
It fails. We can write inequalities and show.
So, did you get the correct solution with the complexity that we want to achieve???
No :(
Can you please tell me the name of the book?
It came in my exam!
Sorry,I didnt see the 7 marks in the brackets.
Sort all the values in increasing order of a_i's. We can then do something like dp[i][j][level] where the dp value denotes the cost for the binary search tree on values from a_i to a_j, with the root at depth = level. The recurrence is dp[i][j][level] = min(dp[i][k-1][level+1] + dp[k+1][j][level]+w_k*level^2) for k from i to j. This is O(N^2) space (we can keep only 2 columns for the level), but O(N^4) time.
I wonder if it's possible in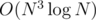 with D&C optimization on each layer of level... not sure but I'll try to prove it.
with D&C optimization on each layer of level... not sure but I'll try to prove it.
I will continue from the solutions proposed by others. Let dph, l, r be the best value we can get if we arrange the numbers indexed from l to r such that the root of the tree is at depth h. The recurrence is, of course:
dph, l, r = minl ≤ i ≤ r(dph + 1, l, i - 1 + wih2 + dph + 1, i + 1, r)
We can build the solution in layers. The last layer is h = n, and here we only need to compute dph, l, l, since we can never build a tree with more than one node at depth n. The same logic applies for other values of h. For example, when h = n - 1, we only need to compute DP values where r - l ≤ 1. In general, we only need to compute DP values where r - l ≤ n - h.
I think that Knuth's optimization trick will work here. This would mean that we can compute each DP state in amortized constant time, so O(n3) total. Since we only need to track the last two DP layers this is O(n2) memory.
Can anyone prove the required property or give a counterexample?
EDIT:
Here's my stress test (100 random samples), and the O(n3) solution passed.