Note that for each hour, there either exists a unique answer or no answer. For instance, at hour 14, the answer is 14: 41 while for hour 17, no answer exists.
Therefore, we can first check for the given hour whether there is a feasible answer or not. If no, then we continue to search for the next hour that has such an answer.
We should first sort the array in an increasing order. Then, for every pair of (ai, ai + 1) with ai < ai + 1, we check whether there exists such an integer x.
The maximum x that can be represented by ai bits is 2ai - 1. Thus, x2 = 22ai - 2ai + 1 + 1. One can check that x2 can always be represented by ai + 1 bits as long as ai + 1 ≥ 2ai.
According to the description of the problem, the graph in fact consists of several simple rings and single links. Thus, we start enumerating from node 1 to node n and for each node that has no input pipe, we visit all the nodes along the pipes while recording the minimum diameter. Finally, print out the recorded results.
We denote the number of his teammates as A and the number of the other students as S. Then, the problem can be solved based on the following three cases.
1) A + S < n - 1: this means that there are not enough students;
2) S < n - 1: this means that the probability is absolutely one;
3) none of the above cases: the answer is just 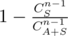 . To compute
. To compute 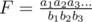 , I usually transform it into F = elog(F). In other words, we first calculate
, I usually transform it into F = elog(F). In other words, we first calculate 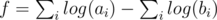 , and then obtain F = ef. I think “log” can guarantee better precision than directly mutiplying all the float numbers together.
, and then obtain F = ef. I think “log” can guarantee better precision than directly mutiplying all the float numbers together.









