Nuruhuhuhu's blog

A Lagrange Multiplier Problem
By Nuruhuhuhu, history, 6 years ago, In English

I have been thinking about this problem for quite some time now but I am stuck and I cannot find a feasible solution for this one. The equation has become really ugly for me and it seems messy. So, please can anyone help me on how to solve this problem? Thanks in advance.

  • Vote: I like it
  • +18
  • Vote: I do not like it

»
5 years ago, # |
  Vote: I like it -10 Vote: I do not like it

Any help now???

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Let x = (x1, x2, ..., xn) represent our solution, xi is the velocity for i-th section (according to the hint, we will always ride with uniform velocity on one section).

It only makes sense to consider solutions with xi > max(0, vi). Also there's always an optimal solution where we use all our energy, because if we have some energy left, we can increase velocity somewhere and we'll arrive faster.

Let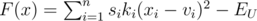 . We'll consider only solutions satisfying F(x) = 0 because we want to use all our energy. Let 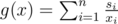. We want to optimize g while respecting the constraint F(x) = 0.

Lagrange multipliers tell us that for optimal solution there exists some λ, such that , so for every i we have xi2(xi - vi)ki = C (where ).

For given C we can solve this equation using binsearch (left side is increasing if xi > max(0, vi). We can also observe that if we increase C, then the solution x(C) will also increase and so F(x(C)) will also increase. So we can binsearch for such C that F(x(C)) = 0 and this will give us optimal x.

→ Reply