Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3650 |
| 2 | Benq | 3582 |
| 3 | Geothermal | 3570 |
| 3 | orzdevinwang | 3570 |
| 5 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3532 |
| 8 | Radewoosh | 3522 |
| 9 | Um_nik | 3483 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 163 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
| Name |
|---|



I liked this round. Generally, the idea of educational rounds is very good. That one in particular expanded my horizons. Usually, when you learn MST, you think: "Why should I bother with Prim's or Boruvka's algo? Just learn Kruskal and forget about the rest". Task G reminds us that every algorithm is important and can have its own unique application.
Before this round, I didn't even know about the existence of Boruvka's algorithm.
Neither did I.
Educational Rounds always teach us about some cool new algorithm or an application of an old algorithm that is not quite popular. :-)
Is Boruvka Algorithm same as Prim's Algorithm ?
FWIW, you can solve this by starting with Kruskal's algorithm too. If you only look at the highest bit at b = 29, and split your vertex set into two halves V0 and V1 (one with all vertices where bit b is turned on, the other all the vertices where this bit is turned off). It follows that internal edges in either V0 or V1 will have bit b turned off, but edges between the two components will have this bit turned on. Thus, if you were to run Kruskal's algorithm you would first enumerate all internal edges in V0 and V1 before considering edges between the two components. It follows that Kruskal's algorithm would first connect all of V0 into a single tree (V1 respectively), and then find a single connecting edge between the two components.
This gives you a simple recursive algorithm: Split on the highest order bit b, solve these two halves recursively (only considering bits < b), and then find the weight of the single connecting edge, i.e. given two sequences of values, find the pair of values with minimal exclusive-or. This last problem can be solved using a very similar recursion.
Code: 32170476
Hey guys! Here are some of my thoughts on the meet-in-the-middle techniques on problem E: http://robezhang.blogspot.com/2017/11/meet-in-middle-technique-on-educational.html Feel free to ask questions and give suggestions!
It is a similar problem but makes it easier to understand this technique.
Here is another problem that is kind of similar: https://www.codechef.com/MAY17/problems/CHEFCODE
Wow cool! It is also a good problem!
Did you remove the post ?
Oh, I've just changed my url for my personal website. You can check this: https://robezh.blogspot.com/2017/11/meet-in-middle-technique-on-educational.html, I hope this is helpful to you.
Hey ! Finally had time to look through your post ! I did find it helpful ... But, you explained how to solve finding four integers who's sum is 0. I wish you explained something about this problem as it's quite challenging compared to that problem. However, I was able to understand your code. :)
Hey, This blog is no more available unfortunately
Why don't you put your implemented codes with the tutorial?I think it will be helpful for many of us :)
For problem C can someone explain this part:
" Write down lengths of segments between two consecutive occurrences of this character, from the first occurrence to the start of the string and from the last to the end of the string."
Let k be the maximal length such that there exists segment of length k that doesn't include character c. You can take all the occurrences of character c and check where this segment can fit. Thus maximal distance between those occurrences and ends of the string will get you maximal k.
Look at my codes for the problem F. I wrote a solution using an algorithm Boruvki but unfortunately it got TLE. Even though my realization is not good as author might have expected to see, I think 2 seconds for the problem which has complexity of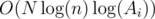 is (very) tight
is (very) tight
Try first sorting numbers. I have no idea why it works, but I also had time limit with same solution and sorting the numbers mad code at least 2x faster.
Doesn't the Boruvka's algorithm work for graphs with distinct edge weights only? In the case of problem G, how is that guaranteed?
It is not guaranteed, hence the warning.
but we should be careful to avoid adding edges that form cycles in MSTCan you please elaborate how is the repetition avoided ??
The problem is with duplicates. Instead of dealing with just weights of edges, consider the pair (w, i) for each edge, where w is its weight and i is the edge index. Now no two pairs are same as each edge has a different index and you can run Boruvka's algorithm as usual.
Code
Got it , thank you.
If I understand correctly, the editorial claims that the answer for B is always n — dx — dy. Can someone prove it mathematically? How about an intuitive proof?
Was just trying to figure out how I can come up with such ideas myself in the future. This sounds like a genius idea to me but I am not sure why it works.
Problem G can be simply solved by trie with 2 keys 0 or 1.
Complexity = O(n * (30 or max(log ai))
Why is the time limit so strict for G? I'm almost using same solution as Editorial, and it takes ~2300MS to pass all test cases, but time limit on CF is 2000MS.
Why A problem have a tag 1600? There is very simple.
Can someone explain 2-D dp solution for problem D. Almost Identity Permutations ?
I love G so so much. I have the same thought of the solution in mind but I didn't think it could run in time. But when I saw the editorial I was very exciting. It actually made me love the CP again even this problem is pretty old. Thank you, the author and Codeforces.
why problem D has dp as one of its tag , it has nothing to do with the dp i guess just simple permutation n combination !!
dp to calculate binomial coefficients OR i guess derangements can be calculated using DP here
Can you explain how to solve this problem in combinatorics?
For problem G (Xor-MST), you don't really need to know Boruvka's algorithm. In fact, I don't really understand what the editorial is saying, but that's okay :D.
Just make a binary trie and all in all of the $$$a_i$$$. Then, for each subtree in our trie, we need to know the minimum cost to to conjoin everything in the subtree. For each node, we store this minimal cost. If we have some node and it has only one child, then the cost for that node is the cost of the child. If a node is a leaf, then it's obviously cost 0 too. If the node has two children, then the cost is sum of costs of children plus cost to join children. To find cost to join children, iterate over stuff in the left subtree and find best corresponding child in right subtree (idk if this makes sense).