This article is about a solution to a variation of 894D - Ralph And His Tour in Binary Country, with (almost) complete binary trees replaced by arbitrary trees. The solution turned out to be more complicated than I thought, so I decided to post it as a separate blog.
The main idea is to fix the LCA, just like the original problem.
Note: We are calculating the sum of all Hi - L, such that
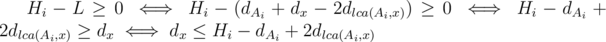
where x is any destination vertex and dv is the distance from the root to the v-th vertex.
Therefore, we could calculate the answer using the following functions:
// dist[v] = sorted list of d_x, where x is any node in v's subtree
// prefsum[v] = prefix sum array of dist[v]
typedef long long i64;
i64 helper(int v, i64 val) {
if(v == 0) return 0;
auto x = std::upper_bound(dist[v].begin(), dist[v].end(), val);
if(x == dist[v].begin()) return 0;
i64 cnt = std::distance(dist[v].begin(), x);
return cnt * val - prefsum[v][cnt - 1];
}
i64 solve(int v, int c, i64 happiness, int start) { // par[root] = 0
if(v == 0) return 0;
i64 val = happiness - d[start] + 2 * d[v];
return helper(v, val) - helper(c, val) + solve(par[v], v, happiness, start);
}
i64 query(int v, i64 happiness) {
return solve(v, 0, happiness, v);
}
We could use this code to calculate the answer for an arbitrary tree, however queries would take 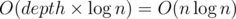 time.
time.
We can speed this algorithm up by using centroid decomposition. We will create a "centroid tree", and create a vector for each node that stores the distances from each node to the nodes in its subtree.
Let d(x, y) be the distance from node x to node y. Then, we need to calculate the sum of all Hi - L such that 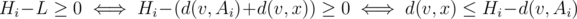 , where v is an ancestor of Ai in the centroid tree, and x is a node in v's subtree, but not in the subtree containing Ai.
, where v is an ancestor of Ai in the centroid tree, and x is a node in v's subtree, but not in the subtree containing Ai.
Note that we can use the exact same helper function to calculate the answer for a single vertex, however we also need to find a way to subtract the answer for v's children. We can reduce subtree queries to range queries on an array using the Euler tour technique.
We also need a data structure that supports the following operations:
1. count(l, r, x): count the number of elements in [l, r] such that ai ≤ x.
2. sum(l, r, x): calculate the sum of elements in [l, r] such that ai ≤ x.
We can use a wavelet tree/persistent segment tree/simple segment tree (offline).
In the following code, let idx[v] be the index of vertex v in the DFS order, and sz[v] be the size of v's subtree in the centroid tree. Then, the code can be adapted for the centroid tree like this:
// we build a separate data structure for every vertex
data_structure DS[MAXN];
i64 helper(int v, int l, int r, int val) {
if(l > r) return 0;
return DS[v].count(l, r, val) * val - DS[v].sum(l, r, val);
}
i64 solve(int v, int c, int happiness, int start) {
if(v == 0) return 0;
int x = idx[c] - idx[v] + 1;
int y = x + sz[c] - 1;
i64 val = happiness - d[v][idx[start] - idx[v] + 1];
return (c == 0 ? helper(v, 1, sz[v], val) : helper(v, 1, x - 1, val) + helper(v, y + 1, sz[v], val)) + solve(par[v], v, happiness, start);
}
i64 query(int v, i64 happiness) {
return solve(v, 0, happiness, v);
}
This solution takes 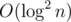 time per query. (
time per query. (solve is called 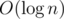 times per query, and every
times per query, and every helper query takes 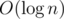 time.)
time.)
Disclaimer: This is the first time I have used centroid decomposition. Feel free to point out any flaws in this approach. I will try to post a full solution later. Update: The initial version stated that this was a solution for arbitrary binary trees. It is actually a solution for any tree.










Auto comment: topic has been updated by f2lk6wf90d (previous revision, new revision, compare).
I don't think it needs to be this complicated, the original solution can be extended to arbitrary tree, you just binary search on the actual node instead of its children, and subtract the overlap from the child you came from. It's also n log^2 n
The problem is that
d[v](in the second code) stores the distances from node v to the nodes in its subtree in the centroid tree, but the distances stored are calculated from the original tree, therefore the data ind[v]andd[par[v]]do not overlap (since a child in the centroid tree isn't necessarily a child in the original tree). Could you elaborate?What I mean is, you don't need centroids. You can just binary search on the parent's array, then binary search on the child you came from with the (distance — (dist to parent)), and when you subtract the two, it will give the non-overlapping portion.
Isn't that O(depth * logn)?
You are right. My bad
Auto comment: topic has been updated by f2lk6wf90d (previous revision, new revision, compare).
100570F — Tree Queries: Basically same problem on general trees, just you don't need to sum the distances. Adding a prefix sum will do that.