Dear All,
How to access to i*th element of a set in c++ effectively (*O(1) or (logN))?
Thanks
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | adamant | 164 |
| 2 | awoo | 164 |
| 4 | TheScrasse | 160 |
| 5 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 8 | SecondThread | 148 |
| 9 | pajenegod | 145 |
| 10 | BledDest | 144 |
| Name |
|---|



There is no documented way to do this. But set is a RB-tree, so you probably can get access to tree's structure and get i-th element in by yourself. I don't think it's a good way
by yourself. I don't think it's a good way
But how to fetch i-th element from RB-tree itself in O(logN) without precalculation?
I don't know, that's true. Well, it looks like one does not simply access k-th element of
set<>What means kth element in Set if the set is unordered?
Surely only ordered sets (for example TreeSet in java) are considered. It looks like set in c++ is implemented in the same way and is ordered therefore.
The trouble is that none of the tree-like data structures available in the standard libraries support a fast k-th element query ("given k, find the k-th smallest of the stored numbers").
The thing you have to add to a canonical balanced tree structure is information about subtree sizes: for each node in the tree, keep the count of elements in the subtree rooted at this node. For a particularly easy-to-implement balanced tree structures, check out splay trees and treaps.
(c) http://community.topcoder.com/tc?module=Static&d1=match_editorials&d2=srm310
You forgot to mention the decreased efficiency of insert/remove for tree with info on branch sizes (up to O(n), I think). You see, it is just a way of precalculation.
More obvious precalculation is, surely, to dump the set into an array and then to make as many queries as necessary.
UPD: I think I am wrong and efficiency of inserting/removing may remain O(logN), sorry.
There is a cheat to access Parent, Left and Right nodes. But i have no idea how to use this information "online". There is problems because of tree modifications — rotations and other balancing stuff while inserting or erasing nodes.
Some discussion about maintaining subtree sizes: http://online-judge.uva.es/board/viewtopic.php?p=42339&sid=06bcbb8c183b8bea4de63a3fa44fb3f2#p42339
Hey! Looks like there's a way to do it after all. Please see http://codeforces.com/blog/entry/11080
No there isn't!. That is another implementation!
You can use C++ SGI STL
tree.For example:
how can we make ordered_multiset ?
Use
pair<T, size_t>as element and give each element an unique id.False. assoc_container.hpp is enough.
I found something pretty crazy while using this data structure for the first time.
I tried to test it a bit before using it in my real problem, and I was surprised to see that it was incredibly slow.
It compiled but, still, it took around 50s just to do
So I gave up and I used a segment tree instead, but in fact the segment tree wasn't perfect for the problem and I ended with only 42 / 140 on this problem (today's COCI#2, problem 5)
Now, I tried to see what went wrong and I found the culprit : -D_GLIBCXX_DEBUG Without that option, I can insert 106 elements in 0.6s, and that's honest for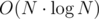 .
.
Morality: never trust your complier options :D
Thanks for this tip, this is totally awesome!
find_by_order takes O(N) where N is size of ordered set
How about binary search? You have lower_bound() for set. Please correct me if I am wrong. The complexity is log(n)*log(L) though. L= range of values in set,n=no. of values in set.
int idx=(int)(S.lower_bound(start,end,value)-S.begin()) if idx>k , search again.
The problem here is
operator -— it works in linear time. Iterators used bysetare bidirectional only, not random access. It means that you can relatively fast increase/decrease them, but you cannot make bigger jumps or subtract them fast than in a linear time (more precisely, in O(answer)).So if we take the lower_bound value from set is O(log n) while taking the position of it is O(n) complexity ?!
Correct.
Thanks for sharing new things ^^ I will keep mind this so that never get TLE for stupid reasoning ^^
Does anyone know of something similar in Java?
Yes. Create Balanced BST <3