Hello Codeforces Community,
I invite you all to join HackerRank's World Codesprint 12 starting on 14 December 2017. The contest duration is 48 hours.
The winners of the contest will win up to 1000USD cash prizes. Also, there are opportunities to win some nice hoodies.
The contest will be rated. If two persons get the same score, the person who reached the score first will be ranked higher. There will be 7 algorithmic challenges in the contest.
The problems are prepared by sreka11, krismaz, nezametdinov, forthright48, muratekici, shashank21j, pkacprzak, Xsquare, danilka.pro, Golovanov399, niyaznigmatul and myself.
Good luck, and I hope you enjoy the problems!
P.S. I hope I got all the CF handles right.











As Hackerrank can't send hoodies to some countries, will people from such countries excluded from list of hoodie winners and first people with >100 rank added?
can anyone give me a hint on how to solve Factorial array(https://www.hackerrank.com/contests/world-codesprint-12/challenges/factorial-array) ,See just for finding the factorial of 10^9 only we would get TLE,how to approach this type of problem , should we use square root decomposition trick, I am having trouble in the range update(+1 for all l to r ) part how to do it efficiently .
How to solve F? I solved it with Heavy-Light decomposition , but I think it has simple solution!
There is an solution with about 10 lines of essential code.
solution with about 10 lines of essential code.
Let's consider any rooted subtree with k vertices. For every integer x define f(x) as the minimum number of operations required to obtain the tree with vertex values nondecreasing root-to-leaves and the root value at least x. It's obvious that f(x) is nondecreasing itself and f(x) = k when x is large enough. Let's define a multiset "up": for every number x we add x to it f(x + 1) - f(x) times (for example for one vertex subtree that would be just one number equal to the number of this vertex a[v]). The answer for the problem would therefore be n minus the number of elements in up[0]. The only thing left is to do a dfs and for every vertex v get up[v] from up[u] of all its children. Not hard to see that by definition up[v] would be a union of all up[u] from which we erase a maximum number which is less than a[v]. Now if we unite these multisets small to big each time the total complexity would be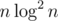 .
.
Nice trick — change values and states of dp! I had to write ~200 lines of code to handle these requests with treap :/
How to solve Breaking Sticks ?
Problem Link
//sorry for my poor English
Solve each a_i independently Now, assume that we are solving a_i = x First, get all the factors of x first. This spend O(sqrt(MAX(a_i))) . Then, we can solve it with dp dp[i] means the best answer for solving a stick which has length i, initially, dp[1] = 1
We can get the transform: dp[i] = max( dp[j]*(i/j) + 1, for all j such that i%j==0 and i!=j )
This spend about O( (factor of x)^2 ) times
you dont need dp, just greedily choose the largest prime factor.
for 12=2*2*3;in increasing order ans=6(1+ 1/2+ 1/(2*2)+ 1/(2*2*3))
It's almost been 2 months, any news about prizes?