→ Pay attention
Before contest
Codeforces Round 940 (Div. 2) and CodeCraft-23
2 days
Register now »
Codeforces Round 940 (Div. 2) and CodeCraft-23
2 days
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 2 | adamant | 164 |
| 4 | TheScrasse | 159 |
| 4 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/19/2024 10:20:28 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Remainder: Contest starts in less than 20 mins.
How to solve the third problem (Automobil) for N,M <= 1'000'000?
Let's calculate the answer first without any operations. Then calculate array R and C, Ri denotes the product of all query's for the ith row, similarly for columns Ci denotes the product of the ith column (I created them lazily with std: : map). Then update the answer according to these, first by rows then by columns. Then update the intersection of the queried rows and columns manually (for example if in one row we multiplied by a and then in one column we multiplied by b then at their intersection we considered this value a + b times but should've considered it ab times), since K is pretty small there won't be many (atmost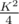 ), so this way we have a O(K2) algorithm.
), so this way we have a O(K2) algorithm.
Ah, I think I got too caught up thinking of how to handle the intersections, should've realised that there would only be ~K2 of them. Thanks!
I solve this problem as follows:
1 Add all values that don't have modifications (blank areas on the image), this step has a time complexity of numbers of queries executed over rows multiply by numbers of queries performed over columns.
2 For each row found in the queries find their corresponding sum and exclude every element that is affected by a column query (red areas on the image). After that add to your answer, this sum multiply by every Y found on the queries that affected the current row.
3 Same as the previous step but by columns.
4 Finally, add to your answer the cells marked in red on the image above.
Time complexity O( K*K ). Memory complexity O( N ).
I hope that this will be useful for you. If you need I can share you my code.
My approach was a little diferent that mavd09 and mraron
The problem is to solve the next summation for each column:
Now if you look that carefully, the terms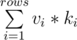 and
and 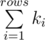 are always same for each j. So you only need to calculate them once. Call the first sumViKi and second sumKi
are always same for each j. So you only need to calculate them once. Call the first sumViKi and second sumKi
Now our answer would be
It can be reduced a little bit. But that's enough for me. So now you only need to precalculate both terms sumViKi and sumKi and the rest is just iterate over columns.
Complexity(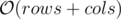 )
)
Code
How to solve D (large) and E?
D:
dpi, j = can i-th player win if (i - 1)-st player said number j. dpi, j = true if
Write array a many times and use some prefix/suffix sums to find that "at least one" thing in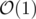 instead of
instead of  .
.
Total complexity: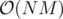 .
.
Code
Thank you. I wanted to do the same thing but defined state a little different so I couldn't do bottom up DP.
I also did this, but will it definitely pass? There are NM dp states, and K processing at each state, giving us O(NMK), or about 1.25 * 1011 operations. Am I missing something?
Edit: I was mistaken, should've paid more attention to the explanation. Thanks for the clarification.
No, process each state is O(1) cause you only need to track the last winning and last losing state.
I think is like dp[i][j] = is turn of i-th animal and the number the previous animal said is j. Now I need to look for a winning or losing state in (i+1)-th animal depending on what kind of animal is animal i and i+1. The first idea of course is to iterate through [j+1 — j+k].
But if you see carefully, the state of [i][j] always is looking in [i+1]. So you only need to know what are the position of the last winning and losing state in [i+1].
Then check if last winning <= j+k or last losing <= j+k depending on the case if i and i+1 are same animal, or not.
AC code
How to solve 140, 160?
Fix the roof i. Let X = Hi, then we should find X that minimizes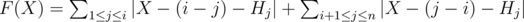 . Let's just simply write it as
. Let's just simply write it as 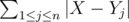 . We can see this is unimodal, and it attains it's minimum when X = (median of Y).
. We can see this is unimodal, and it attains it's minimum when X = (median of Y).
So, for each roof i, we have to find the median of Y, and calculate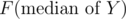 . We will do it in O(lg2(n)) per each i.
. We will do it in O(lg2(n)) per each i.
For the first part, binary search for the answer, and calculate the number of j such that Hj - j ≤ X - i and 1 ≤ j ≤ i, plus Hj + j ≤ X + i and i + 1 ≤ j ≤ n We can maintain fenwick tree for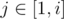 and
and 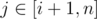 and and answer the queries. Second part don't need binary search, and it's simillar to the first part.
and and answer the queries. Second part don't need binary search, and it's simillar to the first part.
https://ideone.com/5tyUj0
I think it uses the technique from Balkan OI 2011 Time Is Money, but I'm not sure whether it will pass TL (at least it runs very fast on random datas). Whatever, that technique is cool, so I highly encourage you to learn (solution for Balkan OI 2011)
How to find maximum/minimum of unimodal function if there are more xs with same value of F(x)?
Nothing changes. It attains its minimum when X = (median of Y)
I meant for an arbitrary unimodal function (I know it is so for this one).
If you are saying about staircase-like functions, then it don't happen as the function is convex. (I regret "unimodal" is not a good word to explain that function)
And you can't find a maximum in unimodal function. Let f(x) = (x == 12345678). Then you should find 12345678 somehow but it's impossible
Ok, thank you.
For E/140 I sort of did a 2-Dimensional Ternary Search. Not entirely sure both are convex functions. Did anyone else do something like this? Or is there another way to do it>
I doubt that will work. But for fixed i ternary search works.
I generated some random tests in python to check if choosing i is convex and you're right of course, it isn't.
results?
Results are out in evaluator!
How to solve F?
My F/CESTE was Dijkstra's algorithm with vertices (v, time), that the time must be increasing and cost decreasing on each v. It was too slow for O(NM * MaxTime) vertices in the worst case, but luckily passed.
We know that there exists x (0 <= x <= 1) for which the shortest path with weights time * x + cost * (1 — x) gives the optimal answer for time * cost.
Great, then let's find shortest paths with x = 0.
Then, let’s find minimum x < x’ <= 1 such that there is an edge (u, v) such that with weights time * x’ + cost * (1 — x’) Path ((1->u) (optimal for x) -> (u, v)) is better than (1->v) (optimal for x).
And rebuild shortest paths with x = x’.
We will do this process while we can find such x’.
(We can find this x’, just solve some equation a * x + b * (1 — x) < c * x + d * (1 — x) for each edge).
Code: https://pastebin.com/NXPX7Kb5
I think I might have understood what you just said. However, I'm far from being able to prove any of the facts you used. First, let me make sure I understood it the right way: for a fixed x, you compute the optimal path from 1 to all the other vertices, where the weight of a path is defined as time * x + cost * (1 — x) (basically x is a constant that helps in defining the weight of an edge). Now, my problem is: how do you know that there exists a proper choice of x so that the optimal path that you get in that case is also optimal when considering the weight as time * cost? It makes sense intuitively but I can't think of any attempt to prove it. Then, you also count on the fact that you can somehow make leaps that take you to a better answer while increasing the x. This seems even harder to prove, so if you have any idea how to prove any of these facts, I'd be grateful to see them. Aand my last question would be: this is a really strange approach, maybe even more interesting than Alien's trick (which I heard is actually Lagrange multiplier), so I was wondering whether you just came up with it, or you saw something somewhat similar to it in some other problem. If so, could you share that problem with us? Thanks in advance!
To the dowvnoters: Really?:)) It's so funny to see the -7 when my comment also explains part of the solution that some people might not have understood and definitely helped at least those. CF community doesn't cease to impress me