Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | adamant | 164 |
| 2 | awoo | 164 |
| 4 | TheScrasse | 160 |
| 5 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 8 | SecondThread | 148 |
| 9 | pajenegod | 145 |
| 9 | orz | 145 |
| Name |
|---|



Can anyone explain in detail problem c div2?
Wow you got downvoted hard.
Can Some Explain Div2 B with more detail and Example.
Div2 B: You must first build the tree using the normal process and then do a bfs from the root. We're doing a bfs for 2 reasons: 1. because we will colour a subtree only if its parent has a different colour and a bfs is the optimal way to decide that. 2.We need to minimize the number of colourings so its best if we go from top to bottom one layer at a time than any other order.
Thanks For Help :)
Much simpler code... without using bfs or dfs :) 33419770
Maybe I am wrong, but I think you are doing a dfs in your code, you have built the edges and go throw them. You just did not create a separate function and marked vertex already visited.
No I am not using dfs , I am just checking for any given node if there is any first-level descendant which has a different color than its parent,if it is then I increment the answer. In dfs you traverse from one node to its descendant until no further descendants are left to traverse. Hope this helps :)
isn't that called bfs (first level descendants)
You're doing what's written in the editorial itself, adding a 1 to the answer on finding an edge with different colors.
in the div2 if you want color the tree,you can color the tree from Leaf to root, if anyone node's color don't same as its father,you should color the father first, then color this node,so if c[i] != c[fa[i]] the ans need ++ans
finally, the root need color once,so you need ans + 1;
that's all
here is my code http://codeforces.com/contest/902/submission/33418162
Could anyone explain this sentence "if remainders sequence has k steps while you consider numbers by some modulo it will have at least k steps in rational numbers" in problem 901B - GCD of Polynomials?
You can perform Euclid's algorithm using field of remainders modulo some prime number instead of rationals. If at some point you will get B = 0 in rationals, you will also have B = 0 at this step using remainders field. It is possible though that you obtain 0 even earlier but we generate sequence in such way that you don't get B = 0 for n steps modulo prime number 2 thus you won't get B = 0 in rationals during these n steps also.
Hey, what's wrong with this comment? I'm just explaining things :(
I don't know, it's entirely correct... this is how I solved the problem.
Let's say you do one step of the Euclidean algorithm, for polynomials p and q: p = aq+r, where a and r are polynomials with deg r<deg q.
Then, r=p-aq, so (r mod 2) = (p mod 2) — (a mod 2)(q mod 2).
Because the Euclidean algorithm gives unique remainders (up to constant multiples), this means that we can run the two in parallel, and at any given point, the rational polynomial will equal the mod2 polynomial, when reduced.
The algorithm ends when we get r=0. Obviously, if we reach 0 in the actual (rational) sequence, we will also get 0 in the reduced sequence. So the original algorithm will take at least as many steps as the reduced one.
There is a small subtlety — can we reduce any rational number mod 2, like we can with integers? In fact we can, if we don't have an even denominator. It's not hard to see that this never happens, so we are OK.
Do you mean that we will not receive even denominators for any sequence of polynomials or for the sequence of polynomials from the solution of the problem?
Apparently, the first variant is incorrect: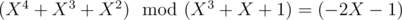 . And when applying the Euclidean algorithm to the pairs like (X3 + X + 1, - 2X - 1) in
. And when applying the Euclidean algorithm to the pairs like (X3 + X + 1, - 2X - 1) in 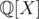 and
and 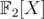 it doesn't seem like steps of the algorithm correspond to each other.
it doesn't seem like steps of the algorithm correspond to each other.
And I still can't find the obvious reason why it is true for the sequence from the solution.
You're right. I'll have to think of it some more. Hopefully it's not a fatal error...
OK I think it still works.
The reason is that in the defined sequence, the degrees decrease by 1. So, you can get extra terms with even coefficients, but the leading term will always have an odd coefficient.
Oh, that makes sense. Thanks!
In Div 2 C, is there any solid prove to this: if there is such a height k that a[k] > 1 and a[k + 1] > 1, then we can create 2 non-isomorphic trees from the current sequence? I mean how can we know if 2 created trees from that sequence are non-isomorphic or not?
You have one longest path from root to farthest leaf. In first tree for each vertex either it is on the path or its parent is at such path. In second tree however it is possible that parent of some vertex still not on longest path.
Take all the nodes in height k+1 and set their parents to only one node of depth k (call it v). This is a rooted tree that has a[k+1]-1 leaves with height k+1.
Now, do the same thing, but take one node in height k+1 and set its parent to another node different from v. This is a rooted tree that has a[k+1]-2 leaves with height k+1. These two trees cannot be isomorphic because the number of leaves with height k+1 are different.
That's why there is the condition of the two consecutives a[i] such that a[i] > 1. If this doesn't happen in the sequence, we can guarantee that there isn't any non-isomorphic pair of trees because:
For every height k such that a[k] > 1 and a[k+1] = 1 (because there aren't consecutive terms greater than 1), picking a parent for this node with height k+1 will not change the isomorphism.
For every height k such that a[k] = 1 and a[k+1] > 1, there is only one possible parent for these nodes with height k+1.
This is a rooted tree that has a[k+1]-2 leaves with height k+1. These two trees cannot be isomorphic because the number of leaves with height k+1 are different..Sorry if i'm wrong, but i think they want to find 2 non-isomorphic trees with same sequence of vertices amount at heights, and i still don't understand why two trees cannot be isomorphic there is the condition of the two consecutives a[i] such that a[i] > 1.
Yes, they want you to give 2 trees (non-isomorphic) with the same sequence of vertices.
The thing is: If there are two consecutives a[i] such that a[i] > 1 then there exists two non-isomorphic trees with the given sequence. In fact, there are some trees with this sequence. Some of them are isomorphic among each other, some aren't. So you just need to pick a pair of non-isomorphic trees.
If there aren't these consecutives a[i], all the possible trees are isomorphic (by the argument above).
To check if two trees are isomorphic, every node in the first tree must have one corresponding node in the second tree. In the example above, there is a node in the first tree with height k and a[k+1] children, and there isn't any corresponding node in the second tree satisfying this (looking at the nodes with height k, there are some with 0 children, one with 1 child and one with a[k+1]-1 children).
But what if in the second tree, there is a node with a[k + 1] children tbat isn't at height k?
The two trees still won't be isomorphic since these two nodes (the node from the first tree and the node you mentioned from the second tree) can't be matched (because they don't have the same height).
The height of a node depends on the node which you chose to be the root doesn't it?
Can we solve 1B through a random algorithm? As we all know, there are hundreds of thousands of possible solutions, and I have no idea on construction of such a sequence, so I used a random algorithm and passed system test.
Here is my code. Hack is welcomed.
Kinda hard to hack if there are 150 possible inputs and all of them can be tested in no time xD
Or even better, you only really need to solve this problem for n = 150. Then you can just work your way down from there.
Not really, intermediate polynomials don't have to have coefficients in {-1, 0, 1} which is kinda crucial here (I think).
I think not if you do it modulo 2
Edit: I agree, but when you figure out that you can do the everything modulo 2 you've practically solved the whole thing
How does the checker work for problem B div 1? It would seem that it might require large (how large?) bignums. I guess it can compute the GCD sequence with a random prime modulus. If it works then great. If not then try another modulus. Once the product of the primes you try is larger than the largest number you'd ever need, I guess you can declare it "good".
It computes pseudoremainders using big integers. Generally size of coefficients grows exponentially but if you divide each term by gcd of coefficients then size of coefficients will grow only linearly of n. I wanted to use prime numbers at first but KAN decided it's not the best idea. However I suppose one needs much smaller number of primes than maximum number to have very high probability of correct verdict...
can someone please explain the idea behind DIV2-D. How fibonacci polynomial leads to the desired answer?
Need it too QWQ
I was upsolving problem C in Div2, using PyPy2 and got a TLE on test case 14. The complexity is O(sum(a)) which is fine, but still got a TLE. However it was accepted when the same code was submitted in Python2 and Python3. I had always known PyPy to be faster than native Python. This has been true in Codechef platform. Can anyone reason as to why it TLE'd in PyPy2?
Python2 Accepted, Python3 Accepted, PyPy2 TLE (14)
This link might help you. Your solution seems to have a lot of string manipulation, and pypy might not be optimizing them as much as cpython, leading to TLE.
For Div1B:
Why does xp_n +/- p_{n-1} always have coefficients in {-1,0,1} for some choice of plus/minus? Is there a reason, or does it just happen to work for the given bounds?
That's tough one to prove strictly. You can check this mathoverflow question.
Spoiler: The answer is by Terry Tao.
Talk about bringing in the big guns...
Is this something you noticed from playing around with polynomials, or did it come up in research or something?
I was thinking on what's the worst case for Euclid's algorithm and apparently found out that this sequence seems to be infinite and has some peculiar properties (like you can choose + or - only at powers of 2, others are determined by that). Surely such approach shouldn't be model solution since it's hard to prove theoretically but there's modular solution which is just fine for this purpose.
I'm not doing any serious research now :)
I was just looking at this year's Putnam problems. http://kskedlaya.org/putnam-archive/2017.pdf
Look at A2... curious isn't it? This sequence appears everywhere it seems.
How is it same?
I guess you have to solve the problem to see that. :D
So was it supposed to just believe in this fact for the model solution? It was hard even to understand, don't think much people could prove this during the contest.
It was supposed to either guess the fact or to use sum modulo 2 which is easy to prove. I doubt that's hard to understand. You want exactly n steps so on each step you want to have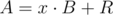 . Obviously, you would like to construct such sequences
. Obviously, you would like to construct such sequences 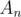 and
and 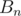 that they're answers for n and first step lead you from
that they're answers for n and first step lead you from 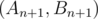 to
to 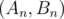 . Thus
. Thus
But this is the same as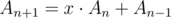 . And it's not about believe because it can be checked in no time.
. And it's not about believe because it can be checked in no time.
Sorry, I somehow haven't noticed second solution in the editorial. Yes, I agree that it's easy to guess and to prove (ability to use - 1 misleads a bit though)
Could you tell me which knowledges are required to understand div2 D's solution?
To come up with the solution like in Div2D / Div1B, I would rather thinking like this:
We already know that it takes two steps to find (x2 + 1, x).
Let's say we need to find the pair that takes three steps. If we call it (A, B), such that the polynomial division A / B will have the divisor equal to x2 + 1 and the remainder equal to x. By that way, we will find (A, B) by continuing finding (x2 + 1, x), which takes two steps. Therefore, it takes three step to find (A, B). Now, as I stated, the divisor equal to x2 + 1, then B = x2 + 1. The remaining task is to find A which has the form of A = (x2 + 1)Q + x.
We can freely choose Q to obtain A. However, to satisfy the restriction that coefficents must equal to - 1, 0, or 1, Q should be x or - x. This solution is pretty close to what is stated in the tutorial. (Mine is pn + 1 = ± xpn + pn - 1. You can easily figure out that if the tutorial's solution satisfies the restriction then so does mine)
Proof by Terry Tao
After we have A and B, we continue applying this algorithm with four steps, five steps, ..., and finally n steps.
Using the characteristic of two consecutive Fibonacci numbers to propose a solution of two consecutive Fibonacci polynomials is, though correct, a little vague (!)
How can you decide when to choose -x and when to choose x?
Just try to assign Q = x and Q = - x. Select the case that brings up a polynomial A that satisfies the coefficents contraint. If both cases satisfy, choose either one of them.
Is it easy to figure out why always either to assign Q=x,Q=-x will lead to a polynomial that satisfies the coefficients constant?
Not really. It’s pretty difficult. Did you check the proof by Terence Tao?
yep, I agree is too difficult. I finally decided to stick with the version of the problem with mod 2. I have heard that it is easier to prove yet I couldn't. Do you know how why the algorithm using mod 2 works?
Thanks a lot, this comment made it seem very simple! (Though, I would be scared to use it because I can't really understand the proof of why it always works.)
but does your method (pn + 1 = ± xpn + pn - 1) guarantee that the leading coefficient will always be 1 (not -1) ??
In div2B why dfs gives the minimum answer.when to apply dfs or bfs i am weak at it plzz help
Okay, I will try to explain. You need to understand that if there is a vertex A and a vertex B, and A is parent of B, you ALWAYS need to paint A first. Why? Because if we paint B, then A, the color of B becomes the same as the color of A (don't forget that A is parent B). So you will need to paint it again, which is not optimal. That's why we need to start painting from the root of tree.
Simple solution for 2B:
AC solution
Div1B can be solved with backtracking — http://codeforces.com/contest/901/submission/33452328
Can someone elaborate on the idea behind div2/E? I still don't understand after reading the editorial.
I too had some trouble understanding it. Convince yourself that there could be no intersecting cycles. You can prove this by contradiction and by considering the parity of length of intersection of the cycle. Now, for every cycle, find the maximum node index in it and the minimum node index in it. Then a segment is good only if it does not contain both the minimum and maximum indices of any cycle in it. So, basically, you have some intervals and now in every query, you are asked to find the number of segments which do not completely cover any of these given intervals.
For reference, I used this code: http://codeforces.com/contest/901/submission/33440062
My solution:
First of all, let's try to reformulate the problem statement using this observation: A bipartite graph is a graph with no odd cycles (Proof). Since the given graph has no even cycles by definition, the only cycles it (and its subgraphs) will have must be odd. Therefore, a subsegment of this graph is bipartite iff it is acyclic. A subsegment of the graph will only be acyclic if it is either a tree, or a forest. Therefore, the problem can be reduced to this: "Find the number of subsegments [x, y] (l ≤ x ≤ y ≤ r) that are forests or trees.".
The second observation is this: If we only take vertex x from the graph and incrementally add vertices x + 1, x + 2, x + 3 and so on, at some point the graph will become cyclic, and from that point on it can never be acyclic again. Let's call that point mx (that is, after the addition of vertex mx, the subsegment [x, mx] becomes cyclic). Note that m1 ≤ m2 ≤ m3 ≤ ... ≤ mn. Therefore, we can use a two pointer approach to calculate m (I used the solution to this problem to remove vertices, see my code: 33436708). The rest of the solution is identical to the one described in the editorial.
Thanks a lot for your answer.
Can you please elaborate a bit more on how you are computing the mx? I referred to your code but could not quite get it. A link to some resource your code follows would also be fine.
All editorials should be written with this level of precision.
Can you explain your implementation?
yep! wait some hours I will make you an explanation
That would be really kind. Thank you so much.
1] We read the tree, CONN vector array stores the connections
2] We run a dfs to search for cycles. The trick is to maintain updated in array vis the deep level of each node that is part of the current track the dfs algorithm analyzes. When we collide with a node member of the track we interpret there is a cycle and with vis[] array we re-build the cycle and detect the min-max values on it (that is what we will need later). We give each cycle a code We add to start[] and finish[] indexed by the min-max value the code of the cycle. (I will explain in 3 why we need them)
3] We start a two-pointers processing to compute mi (that is defined in the editorial as the lower index such that [i, mi] is cyclic) Note that in this case, like f2lk6wf90d says, it is true that a sub-graph is cyclic<=>not bipartite
Also, as f2lk6wf90d says, it can be proved that mi < = mi + 1 1 < = i < = N - 1 (for example by contradiction)
This is the reason now we can use or two-pointers technique or iterate N binary searches. I decided to use two pointers method in the following way:
Use pointers i, j maintaining this invariant [i, j] is cyclic. Iterate over i and update j pointer in each iteration by incrementing it until the sub-graph with nodes of codes [i, j] becomes cyclic thus by definition mi = j. To be able to check if the subgraph is cyclic on each moment we need to make use of start[] vector array, finish[] vector array and min-max values of cycles stored, that gives us the information needed to update if the subgraph [i, j] is or is not a cycle (the interval [i, j] is member of cycle k if and only if i < = mink < = maxk < = j).
Each time when we increment j we check if a cycle k ends in that j value and have already started (mink > = i) (using start,finish vector arrays and min-max cycles data). When this happens we know the graph is cycle.
Also when we increment i we make sure we can check which open cycles stop from existing, using start[] vector array. So I explained almost all details, I assure you that by this process you compute mi
4] Now we have mi computed 1 < = i < = N and this is the hardest part. We precompute prei to make prefix sums.
pre0 = 0
prei = prei - 1 + mi 1 < = i < = N
now 1 < = i < = j < = N
1 < = i < = j < = N
With this information, there is a way to answer the queries in O(log(n)) each one. with tricks obviously.
The query is an interval [l, r] we need to check for every x, y, l < = x < = y < = r if [x, y] is not cyclic (thus bipartite). We iterate over x and get the amounts of y for each x such that [x, y] is not cyclic
To develop the formula we need to analyze two cases:
if for an x mx < = r then there are (mx - 1) - x + 1 = mx - x values of y such that [x, y] is not cyclic.
if for an x mx > r then we've got r - x + 1 values of y.
So for each x we need to compute index u such that u is the lower value such that mu > r We know m is increasing the binary search makes this possible. (We could also use two pointers) And now the answer to the query should be
But by working algebraically we can show it is equivalent to
Using pre-array we can compute the sum so this is O(log(n)) per query that is more than enough to solve the problem.
I have written lot of details. Tell me if I made some mistake. It was long and this could be a possibility.
Thank you very much! Your explanation and your submission were really helpful
In problem Div 1C / Div 2E, can someone please explain, how are we finding the value of mx, in detail. Details in the editorial are not clear to me.
Awesome dude! That's what we need!
In Editorial of Div 1.C, this sentence
To answer the query, we need to take the sum over mxi - i + 1 for those who have mxi ≥ r and the sum over r - i + 1 for those who have mxi ≥ r
I think it should be
To answer the query, we need to take the sum over mxi - i + 1 for those who have mxi < r and the sum over r - i + 1 for those who have mxi ≥ r
then the vertex segment is good - if there is no loopWhat is 'loop'?
then the vertex range (l<=r) is good — if there is no cycle
Can you explain your implementation?
In DIV 1D's description,what does it mean "It is guaranteed that the given graph is connected and does not contain loops and multiple edges." especially 'loop' here, isn't it crashed with the sample?
'loop' which you mentioned is an edge that connect a vertex to itself. But 'loop' in the editorial is like circle.
When they say loop here, they actually mean cycle.
Div 1 B. Can anyone prove that mod 2 of the coefficients of series
p(n+1) = x*p(n) + p(n-1)will give the correct answer? The given explanation isn't very clear. :/I am interested in seeing answer to this question.
problem A(div 2) says It is guaranteed that ai ≥ ai - 1 for every i (2 ≤ i ≤ n). but my submission failed at test 17 which was: 1 10 0 10 so is 0 greater than 1 ? link :http://codeforces.com/submissions/tibialAcorn98
1 10 0 10.
1 — the number of teleports;
10 — the point we want to reach;
0 — a[1]; 10 — b[1].
I can not understand the isomorphic statement . i got WA on test 2 .
How these two trees are isomorphic ?
This was a confusion I had during contest.If u read the question carefully,it is written that if u REENUMERATE the vertices in some way, here REENUMERATE means that assigning the vertices in some order to make the trees equal.
Now if u see ur output, if in the 2nd tree, if I interchange vertices 2 and 3, then it becomes exactly equal to the 1st tree, which shows that they are both isomorphic.
In question U have to output two non-isomorphic trees instead.
Hope this helps :)
if I interchange vertices 2 and 3, then how it becomes exactly equal ? In my output 1st tree -> node 4, 5 connected with node 3
and In 2nd tree node 4,5 connected with node 2 then how it becomes equal ?
By interchanging or reenumerating the vertices I meant that rename vertex 2 as vertex 3 AND vertex 3 as vertex 2.See image
THANKS :)
Can someone please some implementation details about Div 2E? It would be really helpful.
My thinking of why the mod approach works for div2 D:
consider always making A = B*x + C where degree of C is less than degree of B, the problem we will face is that sometimes the result will have coefficients greater than 1, but the leading term coefficient will never be greater than 1, because degree of B*x is higher than degree of C, so the leading term will always be existing once in the expression B*x+C (and so will not be affected by the mod).
now think of A%2, this is = (B*x + C)%2, and similarly B%2 = (C*x + D)%2, and C%2 = (D*x + E)%2, and so on till the rightmost term (E in the last expression) is 0. before we reach this point, all expressions A, B, C, ...etc will always have the leading element coefficient = 1 after and before the mod. so with the mod, we took the same number of steps we would take without the mod.
Div 1.E
Do we need a root of unity of order 2n because when we evaluate polynomial at points {zi} with Bluestein's algorithm we work with elements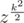 which are in cyclic subgroup of order 2n? (z has order n)
which are in cyclic subgroup of order 2n? (z has order n)
Just making sure I got everything right.
Div-2, Problem(C) : Anyone please clarify me this line ai equals to the number of vertices that are at distance of i edges from root.
Thanks in Advance.
I have a different, possibly unintended, $$$\mathcal{O} \left( N \log N \right)$$$ solution using LCT >.<
Denote $$$f(l, r)$$$ to be the graph produced such that there is an edge between $$$u$$$ and $$$v$$$ iff there is an edge between $$$u$$$ and $$$v$$$ in the input graph and $$$l \le u,v \le r$$$.
Observation 1: A graph is bipartite iff it has no odd cycles. Since the graph is guaranteed to have no even cycles, this means that if $$$f(l, r)$$$ is good iff it's acyclic.
Observation 2: There's a sort of monotonicity going on here: if $$$f(l, r)$$$ is valid, then $$$f(l, r - 1)$$$ is also valid.
Observation 3: We can use a two-pointers approach, in lieu of observation $$$2$$$, to find the maximum $$$r$$$ for which $$$f(l, r)$$$ is valid. If we can increment $$$r$$$ while still maintaining acyclic, then do so. If we can't, increment $$$l$$$.
The key issue is how we can increment/decrement $$$l$$$ or $$$r$$$ and still check for cycles. LINK CUT TREE. To see if adding $$$(u, v)$$$ will form a cycle, check if $$$u,v$$$ are in the same connected component (can be done using link cut). To remove vertices adjacent to $$$l$$$, well, "cut" those edges. To add vertices adjacent to $$$r$$$, well, "link" those vertices.
Observation 4: Querying is simple. It' just $$$\sum_{i = l}^{r} min(arr[i], r) - i + 1 = -\frac{(l + r) \cdot (r - l + 1)}{2} + r - l + 1 + \sum_{i = l}^{r} min(arr[i], r)$$$. To compute $$$\sum_{i = l}^{r} min(arr[i], r)$$$, use the fact that $$$arr$$$ is increasing. Binary search for first time something is less than $$$r$$$: on this interval, it's just a range sum. Afterwards, when everything is greater than $$$r$$$, keep adding $$$r$$$.