Hi, i'm trying to solve the following problem : Given 1 ≤ m ≤ n ≤ 100000 , calculate:
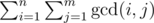
If n = m is kind of easy, but i can't think of anything for n > m.
PS:I think an 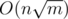 solution or anything similar can be squeezed to pass TL , if you have any idea please share :D
solution or anything similar can be squeezed to pass TL , if you have any idea please share :D











This can be done by phi function. kind of similar question good explanation link. If you understand that then this is pretty easy
I don't see how they are related (with n != m), can you please elaborate? I already know how to solve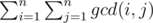 which is kind of the same as solving the LCM one..
which is kind of the same as solving the LCM one..
Can you Please give me the link of the question.I have an Idea.I want to check if it is right or wrong.
You can submit here.
If we calculate for n=4 and m=5 then your given expression(in this post) sums to 28.But In the problem link you gave me the answer should be 36.I don't think the problem is asking to find the above expression.
Still if you want to calculate the above expression i can tell you
The problem is a variant.. It's easy to see that the problem asks for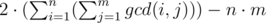 please read carefully, and the answer should be 28 for n = 4 and m = 5 , a simple brute-force can verify this.. Please share your ideas, any help is welcome.
please read carefully, and the answer should be 28 for n = 4 and m = 5 , a simple brute-force can verify this.. Please share your ideas, any help is welcome.
Go through the link. Handwriting is pretty bad.If any doubt remains feel free to ask
dp[i] = number of pairs (a, b) that gcd(a, b) = i. It's very easy to calculate it in descending order: for i from min(n, m) to 1.
Apparently
You can precompute the values of ϕ in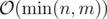 using a sieve and then compute the sum in
using a sieve and then compute the sum in 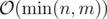 , which should be fast enough.
, which should be fast enough.
I think you can use the technique from here to compute the sum in , similar to example two on the linked page, you just use the harmonic lemma for both n and m.
, similar to example two on the linked page, you just use the harmonic lemma for both n and m.
Thanks for your reply, this is exactly what i'm looking for, but seems that i'm unable to prove :/ Any hints in how to prove this? Thanks anyway!
Turns out it's just a bunch of calculations. (Let's hope I didn't make to many typos.) If some step is hard to understand, you might want to look here for some simpler examples.