We should keep updating the maximum and minimum values that we have obtained, and increase the counter according to the requirements.
The main idea is greedy algorithm. We sort the cards in a decreasing order of the number of cards that we can further check, and if the numbers are equal, we sort them in a decreasing order of scores. After sorting, we start from the first card and implement the simulation step by step.
Note that any single letter will not appear in more than one constraint, and thus we can deal with the constraints one by one in an independent manner.
Given a constraint, i.e., two letters x1 and x2, we can find all the consecutive intervals [l, r] so that only the two letters are included. For each interval [l, r], we also count the number of letter x1 and x2 as n1 and n2, respectively. It is obvious that we must either delete all x1 or all x2, since otherwise we can always find two neighboring letters of x1x2 or x2x1. Thus, we should delete the letter corresponding to min(n1, n2) for this interval.
A key observation is that 100000 < 2 × 3 × 5 × 7 × 9 × 11 × 13, implying that any integer that does not exceed 100000 can have at most 7 (strictly speaking 6) different prime divisors.
Based on the above observation, we can implement sieve function to find out all the prime integers and also the prime divisors that each integer has. Then, when an integer is added, we find all its prime divisors and check whether these divisors have already appeared before or not, to determine whether this integer can be successfully inserted or not. If an integer is deleted, we should delete all their prime divisors at the same time.
In other words, we can maintain multiple sets d[i], so that d[i] (it is a set) contains all the integers which have been added and have such a prime divisor (this implies that i should be some prime integer), and update these sets whenever an integer is inserted or deleted.
The idea is a little weird (from the tutorials). The essential issue is to determine whether two sets contain exactly the same integers or not.
We find a prime integer, for instance 29, and assign integer i with a weight 29i. Then, for some set containing integers (i, j, ...), we compute its hash value as i × 29i + j × 29j + ... (if we use “long long int”, the modulo operation is automatically implemented). Two sets are exactly the same if they have the same hash value. For simplicity, we use h[i] to denote the hash value of the set that node i has.
Note that we should check every pair of two nodes. We can divide all the pairs into two types, one containing those which have direct edges, while the other one containing those that do not have direct edges.
For the first type, we can check each of them in the order of given edges. Be careful that we should delete the hash value of the neighboring node from the total hash value.
For the second type, we can sort h[i] in an increasing order, and find out all the intervals of h[i] that have the same value. For instance, some interval contains k same values, and then it contributes 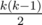 to the final answer.
to the final answer.









