Hanoi Tower Troubles Again is a problem I recently discovered in "Programming Challenges" by Skiena and Revilla. It seems to be quite popular, because some (bad!) solutions can be found on various websites. I want to proof a nice explicit form here (see below).
It's trivial to solve this using (greedy) simulation (*). But Skiena and Revilla provide a short hint:
Can the constraints be usefully modeled using a DAG?
I thought about constructing a DAG where longest path corresponds to optimal solution. Unfortunately, my best approach is to use (a1, a2, ..., aN) as state where ai denotes number on ball on top of peg i; exponential number of vertices is bad. How to use this hint in a suitable way?
Considering small cases, one find the answers
1, 3, 7, 11, 17, 23, 31, 39, 49, 59, ...
for 1, 2, 3, ... pegs respectively. I conjecture that 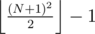 is the answer in general.
is the answer in general.
Crawling through roughly a dozen websites with trivial simulation and no comments, I encountered a chinese article where a recurrence relation is given but not proven: h(1) = 1, h(2) = 3, h(i) = h(i - 1) + i for even i and h(i) = h(i - 1) + i + 1 for odd i.
Finally, there are two questions:
How to utilize a DAG suitable?
How to prove the recurrence and/or explicit form (if correct)?
Any kind of help and interesting ideas are appreciated!
(*) It's not immediately clear that solution is bounded and greedy simulation is correct.











Auto comment: topic has been updated by neutron-byte (previous revision, new revision, compare).
Why couldn't we place infinity numbers of ball on one peg? I didn't see any constraints about maximum number write on a ball, or did i miss something?
Assume infinite number of balls is possible. If there are N pegs, consider placing ball with number 2N2 on some peg. The smallest number which can be placed next on this peg is 2N2 + 4N + 1. Thus, we have to do the next 4N moves on the remaining N - 1 pegs. Similarly, we pair 2N2 + 1 with 2N2 + 4N, 2N2 + 2 with 2N2 + 4N - 1, ... , 2N2 + N - 1 with 2N2 + 3N + 1. Now, all N pegs are blocked, because all next possible numbers are greater than 2N2 + N. Thus, we established an upper bound of 2N2 + N - 1.
Do a binary search for the answer k. This way the problem can be reduced to the question "Can k balls 1, ..., k be placed on n pegs?".
The reduced question can be solved as a flow problem on a DAG. There is a vertex a for every ball a. There is an edge a → b iff b can be placed on a. (i.e. a < b and a + b is a square.) Every vertex has capacity 1 (As every ball gets placed once.). Each vertex is connected to the source and the sink. The balls can be placed iff there is a flow of value at most n that saturates every edge corresponding to a vertex capacity. (The balls placed on a single peg correspond to a path in the flow decomposition of the flow. There are no cycles in the decomposition as the graph is acyclic.)
On way to solve the DAG model is min-cost flow. The edges corresponding to vertex capacities have cost - 1, all other edges have cost k. The covering flow exists iff there is a min cost flow of flow value f ≤ n and of cost - n. This min-cost flow can be found in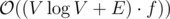 , so the total runtime is
, so the total runtime is 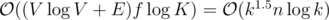 .
.
The DAG model can also be solved by bipartite matching. There are two vertices a, a' for every ball a. There is an edge a → b' iff b can be placed on a. The balls can be placed iff there is a matching of size at least k - n. (The matching edges correspond to the saturated edges in the min-cost flow problem.) The total runtime is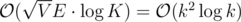 .
.
Your formula for h(k) is know on OEIS. It can probably be proven by induction on "h(k) = ... and there is an optimal solution such that the balls that are on top of the pegs have got the highest n numbers.