Hi. I am trying to solve this problem.
For convenience, I have summarised the problem statement below:
Problem Statement
We are tasked to arrange X Apples, Y Cherries and Z mangoes on a line, Compute the number of valid arrangements (modulo 1e9 + 7). All X + Y + Z fruits must be used in a single arrangement.
A valid arrangement is defined as an arrangement in which no two fruits of a similar kind are adjacent (no wraparound).
Constraints: 1 ≤ X, Y, Z ≤ 2e5
Time limit: 2s
Example
Example of a valid arrangement for X = 2, Y = 2, Z = 2 is:
Apple Orange Cherry Apple Orange Cherry
Example of a invalid arrangement for X = 2, Y = 2, Z = 2 is:
Apple Apple Orange Cherry Orange Cherry
My analysis
If the constraints were smaller, an obvious 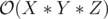 dynamic programming solution would suffice. However, the large constraints here seem to point towards a combinatorics solution (which I cannot figure out).
dynamic programming solution would suffice. However, the large constraints here seem to point towards a combinatorics solution (which I cannot figure out).
Could someone please advise me on how to solve this problem?











can we swap two same fruits? For example :
1Apple 1Orange 1Cherry 2Apple 2Orange 2Cherry and 2Apple 1Orange 1Cherry 1Apple 2Orange 2Cherry
Like this
You can lock one of the fruits. For example if you lock the apples, arrangement would be like ...X...X...X...X... and between those X's YZY..Z or YZY..Y or ZYZ..Z or ZYZ..Y. And you have to find how many ways you can put those ...YZYZYZ... between those X's.
Hmm. How would you count the number of YZ between the Xs? I think that this step itself is non-trivial.
tourist Hey help this guy.
Here is the tutorial of this problem, seeing the problem I.
tutorial
And here is an accept code written by me a long time ago...
https://ideone.com/0gpXJI
Hi. I have read the tutorial before. However, the important formula on page 37 is not explained. Did you manage to derive it on your own? If you did, how did you manage to derive it?
Please advise.