Hello!
Topcoder SRM 728 will be held tomorrow (January 25, 2018).
See what time it starts in your area.
I'm the writer. Everyone is welcome to participate!
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Hello!
Topcoder SRM 728 will be held tomorrow (January 25, 2018).
See what time it starts in your area.
I'm the writer. Everyone is welcome to participate!
| Name |
|---|



Tourist these days be like
Image not working :/
Tourist banned that... Someone still believes that there is no censorship on CF?...
Looking only this as an example, I strongly believe that there is no censorship on CF.
Reminder: The contest starts in less than 4 hours. Registeration has started.
If you are first to compete and don't know how to use applet, I suggest downloading applet from https://www.topcoder.com/community/competitive-programming/ and see https://www.youtube.com/watch?v=A5vnkkFGOo0 (of about first 20 minutes).
Use IcedTea in Linux for running applet.
How to run under proxy server?
arena is not working properly:
screenshot
I didn't experienced. Did you try once more?
yeah, it works fine now
Arena not working for me. The same with web arena
Is it possible to solve d1-500 with factorial polynomials?
????? Am I missing something????
http://apio-olympiad.org/2016/tasks/boat/descriptions/en.pdf
I think you are not missing anything, and this problem is indeed very similar to today's Div1 Medium. Unfortunately, I haven't been checking APIO problems since I graduated from high school :(
Sorry about that.
Well, individuals can make mistakes, but I don't understand that you didn't had any testers pointing out that.
But whatever, it seems nobody remembered that APIO problem (and I'm really surprised about this. Why guys?????) I'm pretty sad to miss a trivial 497 points.
How to solve Hard? I've seen that the twirl operation actually just allows you to consider basically isomorphism only for even permutations. And it's obvious how to count the number of isomorphism classes if it weren't for this parity stuff. But it just seems impossible to tackle...I'm really curious to see the solution
The usual way to find the number of equivalence classes under a group of actions — Burnside's lemma.
Shit...I need to learn that. I've kept procrastinating it. Do you have any good tutorial?
Here is a short summary of solutions. Have fun!
Generate all stick lengths obtainable from every ai, along with the number of steps required to obtain it. From all lengths obtainable from all ai, pick the one obtainable in the smallest total number of steps.
The main question is: how many distinct stick lengths are obtainable from a stick of length L?
In fact, this number is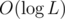 . It can be seen as follows. While L is even, divide it by 2 until it's odd. When it's odd, we'll have two possible stick lengths on the next step, let's denote them by X and X + 1.
. It can be seen as follows. While L is even, divide it by 2 until it's odd. When it's odd, we'll have two possible stick lengths on the next step, let's denote them by X and X + 1.
What stick lengths are obtainable on the next step? They are X / 2, (X + 1) / 2 and (X + 2) / 2 (integer division). Clearly, X / 2 and (X + 2) / 2 differ by exactly one, and (X + 1) / 2 is equal to one of them. Thus, on the next step, we'll still have only two possible stick lengths. Since the number of steps is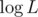 , the number of obtainable stick lengths is at most
, the number of obtainable stick lengths is at most 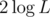 .
.
This is a DP problem. The only trouble is that Ai can be up to 109.
Divide all integers from L1 to Rn into segments such that all integers in this segment belong to the same set of ranges [Li;Ri]. For example, if the ranges are [1;10], [3;10] and [8;15], then we'll form segments [1;2], [3;7], [8;10] and [11;15]. Clearly, we'll form at most 2n such segments.
Now, for every i, instead of deciding the value of Ai, let's only decide which segment it belongs to. Since Ai must be an increasing sequence, corresponding segment IDs must be non-decreasing.
For a fixed assignment of Ai to segments, how many ways are there to actually choose all Ai so that the conditions are satisfied? Well, it's the product of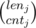 , where lenj is the length of the j-th segment, and cntj is the number of Ai belonging to the j-th segment.
, where lenj is the length of the j-th segment, and cntj is the number of Ai belonging to the j-th segment.
This leads to a DP solution. Let fi, k be the number of ways to assign the first i numbers to the first k segments. Transitions are done by looping over how many numbers are assigned to the next segment. The complexity is O(n3) (if you precalculate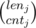 in advance or quickly calculate them during the process).
in advance or quickly calculate them during the process).
The solution is a somewhat straightforward application of Burnside's lemma.
For every even permutation p, we count the number of graphs left invariant by p. Then we know the answer.
Let's count such graphs for a given p. Suppose we have edges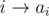 for all i in our directed graph. Fix some i. We have an edge
for all i in our directed graph. Fix some i. We have an edge 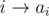 . Since the graph is left invariant by p, we must have an edge
. Since the graph is left invariant by p, we must have an edge 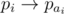 in our graph. Similarly, we must have an edge
in our graph. Similarly, we must have an edge 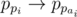 too, and so on. Suppose that i belongs to a cycle of length ki in p. Then, we must have an edge
too, and so on. Suppose that i belongs to a cycle of length ki in p. Then, we must have an edge 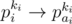 . Since pkii = i, and we only have one edge outgoing from each vertex, we must have pkiai = ai. Thus, ai must belong to a cycle in p of length kai which is a divisor of ki.
. Since pkii = i, and we only have one edge outgoing from each vertex, we must have pkiai = ai. Thus, ai must belong to a cycle in p of length kai which is a divisor of ki.
This is a necessary condition. But if on every cycle in p we pick one i and choose ai so that this condition is satisfied, then we can deduce the outgoing edges from all vertices on this cycle, and the condition will be satisfied for these vertices, too. It can be seen that this is also sufficient -- with the condition satisfied, there is a bijection between the original and the permuted vertices and edges, so that's an automorphism.
Hence, once we know the lengths of cycles in p, we can easily count graphs left invariant by p in polynomial time. Every distribution of cycle lengths is a partition of n, and there are not too many partitions for n ≤ 50, so we can try them all.
For every element of S, apply halving to it while it's larger than T. If it turns out to be equal to T after that, add 1 to the answer.
This is a DP problem.
Let fi, j be the number of increasing sequences A1, A2, ..., Ai such that Ai = j. Clearly, if j < Li or j > Ri, then fi, j = 0. Otherwise,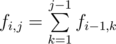 .
.
The problem is that this solution is too slow -- it works in O(n·max(Ri)2).
To fix that, note that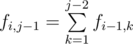 . Thus, if both j and j - 1 belong to [Li;Ri], then fi, j = fi, j - 1 + fi - 1, j - 1. We can calculate fi, Li first in O(Li) time, and then calculate fi, j for j from Li + 1 to Ri in O(1) time each.
. Thus, if both j and j - 1 belong to [Li;Ri], then fi, j = fi, j - 1 + fi - 1, j - 1. We can calculate fi, Li first in O(Li) time, and then calculate fi, j for j from Li + 1 to Ri in O(1) time each.
This way, the solution works in O(n·max(Ri)), which is just enough to get accepted.
The key insight is: by applying twirls, we can permute the labels of the graph almost arbitrarily. In fact, we can apply any even permutation to the labels, since every twirl is equivalent to performing two transpositions.
The solution is: loop over all even permutations of length n and permute vertices of the graph according to them. Count the number of distinct graphs obtained using any equivalent of hashset. The complexity of this solution is about O(n!·n).
It's also possible to do the Div1 1K in polynomial time (code in the practice room):
That tells you the number of equivalence classes under isomorphisms, but not trisomorphisms (even permutations). Those equivalence classes for which there is an auto-trisomorphism should be counted once, those without an auto-trisomorphism should be counted twice. To count the latter, run through the same DP again, but this time exclude any rooted tree/graph that has an auto-trisomorphism e.g. for a tree, reject it if it has two isomorphic subtrees of odd size.
My implementation is O(N3), but I wouldn't be surprised if it can be reduced.
Sadly this was far to complicated to get right during the contest.
It's also possible to the div1 med by reducing it to this problem: http://codeforces.com/problemset/problem/559/C.
For instance, replace L[i],R[i] with L[i]-i, R[i]-i, respectively so we are looking for non-decreasing sequences. For each interval L[i], R[i], we can add the points (i, R[i]+1) and (i+1, L[i]-1). Then, we just need to find the number of paths from (0,0) to (n, R[n-1]) that go only go down/right and don't touch any of the given points. This is a bijection, since we can take the column where we go from row i -> row i+1 to be the i-th number in our sequence. This can be done in O(n^3) if you don't preprocess factorials, but I'm not sure if you can get to O(n^2) with some smarter pre-processing.
If I understood you correctly, I think there is a bijection iff after doing your changes for L and R arrays, we need to make L non-decreaasing (each L[i] is the maximum of all L[j] for j<=i) and R non-decreasing (each R[i] is the minimum of all i such that j>=i) to make the bijection true, and also making those changes in that way won't change the answer.
Imagine the case where all L[i] are very large except for the last one is very small, there will be a path that go down early at first row (after a few steps), and keep going down, and at row n turn right, and you will avoid all L points since all of them is large except the last one (will be also avoided as L[n-1]-1 is smaller than index current column) , you can also find similar case for R.
But I believe if you made L non-decreaasing and R non-decreasing in the correct way the bijection will hold.
Anyway, I really like your solution a lot ^_^
Thank you :)
This question is not about SRM 728. In topcoder is it possible to see SRM announcement at least 1/2 day(s) before? I used to see about SRM in arena in the day of contest. Due to this I miss SRM frequently.
Pro Tips:
Now you have a schedule on SRM 729 and SRM 730:
SRM 729: February 10th, 12:00-13:35 (UTC -5), writer is Errichto
SRM 730: February 20th, 07:00-08:35 (UTC -5)