→ Pay attention
Before contest
Codeforces Round 940 (Div. 2) and CodeCraft-23
43:53:21
Register now »
Codeforces Round 940 (Div. 2) and CodeCraft-23
43:53:21
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 2 | adamant | 164 |
| 4 | TheScrasse | 159 |
| 4 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/19/2024 21:41:39 (j2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











How to solve F?
Anybody? Seems like a nice problem
Well during the contest I had the following idea that gave me 112/160 points. I already sent my idea to someone else so I guess I'll just copy-paste it here:
My solution is not completely correct, as I got 112 points out of 160 (it was a strong greedy that I did not prove and turned out as incorrect (or I just had a bug, idk)).
1) If we visualize the children as nodes in a graph, and there's an edge between every pair of (child, best friend), then because every node has exactly an indegree and outdegree of 1, this graph is just made of several components (can be 1 component) of simple cycles. So we can pick which values to give to every cycle.
2) Let's say we gave every cycle the values we want to give to its nodes. How do we distribute them optimally? Claim: We sort the values and we go by this pattern (I'll write the indicies of elements we take after we sort, and we'll assign them to the cycle one next to the other):
0 2 4 6 8 10 ........ 9 7 5 3 1. (note that because it is a cycle, the last value (at index 1 here) will be also connected to the first value (at index 0 here)).
Proof: Let's denote in the above array, D[i] = A[i] — A[i — 1]. Note that all D[i] are positive as we sorted the array. So, if we go by this pattern, the maximal difference between the pairs of adjacent nodes in the cycle is: max(D[1] + D[2], D[2] + D[3], D[3] + D[4], D[4] + D[5], .....).
It is basically the maximal sum of 2 adjacent values in the array D (you might want to draw the pattern on paper and see for yourself). Without loss of generality (and to make explanation simpler), let's suppose the maximal sum is, for instance, D[5] + D[6]. This is equal to (A[5] — A[4]) + (A[6] — A[5]) = A[6] — A[4].
We would want to get rid of this difference. In the pattern, let's split it to 2 halves: the increasing half, and the decreasing half (I'm sure you can understand what I'm saying here).
In both halves, in order to get rid of this difference we need to take the element A[5]. Why is that? Because if we don't take the element A[5] in, say, the first half, then we must have took 2 elements A[x] and A[y] right next to each other, so that (x <= 4, y >= 6): A[y] — A[x] >= A[6] — A[4] in that case.
However, we can't take the element A[5] in both halves, since we must take every element exactly once. So this proves the pattern is optimal. From now we'll consider the whole array A, from which we take elements, as sorted.
We will also precompute: ans[i][j] = this maximal sum for a subarray from index i to index j in the array A. We can easily compute it in O(n^3) with pure bruteforce, and also easily in O(n^2) but it doesn't matter really.
3) Now let's consider the cycles by just their sizes. So now we have a group of values that denote sizes, and their sum is N. We would like to give to every cycle some elements from the array A, the number of elements should be equal to its size.
Claim: For a size of cycle X, we want to pick from the array A a subarray (contiguous) of size X. I did not prove this claim though, it's very intuitive.
4) This is the greedy part: we need to decide for every size, the subarray we give to it. I tried to come up with some kind of DP, but failed (at least one that fits in the time limit). So I decided to do some binary search over the answer to the problem:
Note that: ans[i — 1][j] <= ans[i][j] <= ans[i][j + 1]. We will use this property. Let's say in the current binary search iteration we have our "mid". First off, we insert all sizes of cycles into some multimap (first is size, second is the index of the cycle so that we can reconstruct).
We start from index 0, and we binary search on the largest X such that ans[0][X] <= mid. Once we find this X, we find the largest size in the multimap that is at most the size of this subarray, and use this size S for the subarray ans[0][S-1] (if there is no such size in the multimap, then we say there's no answer with that mid). Then we remove this size from the multimap, set our start index from S, and repeat the process.
The final part can be done with dp[{c1, c2, ..., cn}] is the minimum cost to distribute first s = c1 + 2c2 + ... + ncn bag of candy (assume that we sorted the bags in increasing order) into a set of cycles, with ci cycles of size i. An important observation is that the number of dp state is not large (which could be found out using another dp).
I learned this solution from I_love_tigersugar. Feel retarded for not realizing that the number of dp states is small.
I wonder if there is a polynomial solution to this problem.
As the author of the problem, I can confirm that this was indeed the intended approach.
Also note that although the first three observations made by Noam527 are correct, the last part is not. As a counterexample, consider a permutation with cycles of sizes 3, 3, 4 and let the quantities of candies be 1, 1, 1, 1, 1, 5, 10, 10, 10, 10. In this case, the greedy algorithm fails to produce a valid distribution when "mid" is equal to 5 in the binary search. I apologize for the weak test data, I was not aware of this particular approach.
As a final remark for the mathematically-minded, it can be shown that the complexity of the solution is roughly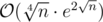 , although it is much less in practice. I doubt that a polynomial solution exists.
, although it is much less in practice. I doubt that a polynomial solution exists.
Can you give me a 100-point solution or an AC code. This is a nice problem which seems had a clever trick, but I can't solve it.The state of my dp is too large.
PS:I can't see your dp in your discussion,it showed "Unable to parse markup [type=CF_TEX]"
Thank you very much
The maximum number of states for the DP function is 4230144 in case we have 16 cycles of 1 node, 8 cycles of 2, 5 of 3, 3 of each size 4 and 5, 2 cycles of 6 and 7, and one of each size from 8 to 12.
abeker I wonder if you put this test in the dataset :D Thank you for such a nice problem with a lot of greedy observations, but ends up with a DP approaches :D
Yes, I did include this test in the dataset, along with some other tests with a large number of states. I'm glad to hear you liked the problem :D
Why would this code get SGKILL for C?
Memory limit on C is 128MB, your dp array takes over 300MB.
B and C today is harder than usual, but D is easier than usual (and easier than C).
Btw, how to solve E? I can prove that answer always exist due to Dirichlet theorem, but can't come up with anything else.
UPD: Turned out C is really harder than D (D has 39 AC, but C only has 32).
I got 28 points at first by submitting a solution where I wrote
binstead ofb - 1, which would've gotten the 140 points (I checked right after the results). I did not prove anything, it was just pretty heuristic.I had an array of vectors, in which cell number X contains the indicies of values in the progression with digit sum X (in base B). Once some cell in that array was a vector of size M I outputed its elements. So what I did was:
if B < 50, go over the indicies in bruteforce (by order), and keep pushing back to the vectors. The running time of this should be worstcase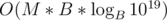 if I'm not wrong (by pigeonhole principle; The maximal digit sum for a base B should be approximately
if I'm not wrong (by pigeonhole principle; The maximal digit sum for a base B should be approximately 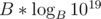 ).
).
otherwise, I did something very similar; I started with the index = 1, but instead of doing jumps of 1, I did jumps of B - 1 (in the submission of 28 points I accidentally did jumps of B). Resubmitting after the contest, this gave me 140 points.
f(x) — sum of digits of number x.
f(x) % (b — 1) = f(x + b — 1) % (b — 1) (in base B)
our sequence is (c * n + d), where n = k * (base — 1), so f(c * n + d) % (b — 1) = f(d) % (b — 1).
Complexity: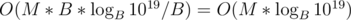
I am the author of the problem.
In essence, what you wrote in the last paragraph is the official solution. Dirichet's pigeonhole principle, when increasing the index variable by 1, gives worst-case complexity of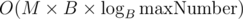 , where the maximal number is a polynomial of the numbers in the input.
, where the maximal number is a polynomial of the numbers in the input.
One can notice there are far fewer "boxes" while increasing the index by B - 1, because every integer is congruent to the sum of its digits in base B modulo B-1. This brings the complexity down to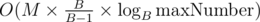 , which should pass for all B because
, which should pass for all B because 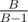 is close to 1.
is close to 1.
(Note that the above approach can be implemented using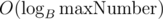 memory.)
memory.)
Does anyone know of an another approach that leads to a correct solution? There are many other methods, but I am not aware of another solution with a time complexity that does not depend on B heavily.
I'm glad to know I was at least close to the solution :).
Also, how do you actually propose a problem for COCI?
Nice solution and nice problem.
Be confident! No one solved perfectly it during contest. You had gotten almost every main ideas of this.
How to get full marks on D? I was only able to come up with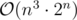 bitmask dp.
bitmask dp.
You just needed to do 2 observations, and then you can do DP in O(n2): First off, for any point (x, y), we can change it to (abs(x), abs(y)). So from now we'll suppose all points have positive coordinates.
Secondly, if you have a pair of points (X1, Y1) and (X2, Y2), so that X2 ≥ X1 and Y2 ≥ Y1, then you can completely ignore point (X1, Y1), because any rectangle covering the other one will cover this one too.
So now, what I did is first maintaining a map that contains the maximal Y value for all points with the same X value. Note that the map will also have the points in increasing values of X. Then, you need to get some kind of a decreasing sequence (decreasing in the Y value) of points:
Let's say we'll build this sequence on some vector A. So for every point K from left to right, we will pop the elements from the back of vector A as long as the element at the back has a Y value lower than or equal to the Y value of point K, and then you push point K to the back of the vector. Now our task is reduced to just making rectangles for these points in vector A. This algorithm has a running time of O(n).
Then, notice that every rectangle you create will cover a contiguous segment of points in vector A. I will leave the O(n2) DP solution for you.
We can make complexity O(nlogn) with CHT or LiChao segment tree, am I correct?
I think it would fit better to D if limits were big enough :)
If we'll denote X(A), Y(A) as the X and Y values of point A respectively, then the recurrence is:
DPi = min1 ≤ j ≤ i(DPj - 1 + 4 * Y(Aj) * X(Ai)).
This falls under the CHT category (though I think if this had to be the solution, it wouldn't fit for a D problem... at least an E).
Thanks, got AC. Why do we need to maintain maximal Y value for all points with same X? If there are two points (x, y1) and (x, y2) with y2 > y1, can't we forget about (x, y1)?
This is exactly what we're doing; we're taking the maximal Y value, which means we ignore all points with equal X value but lesser Y value.
My O(n2 * 26) solution to the problem C gets TLE at two last tests. What is the probably reason? (link)
Use scanf and printf for c++11
Got AC, thanks :)
https://hastebin.com/nilitahoju.cpp My O(n*26*26) solution on C got TLE on the last 2 tests. How can I improve my code?
I also want to ask how to solve B. Thanks.
Your solution is not O(n * 26 * 26) it is O(n3), so TLE is justified