Hi :)
Here is the editorial for round #148. I just tried to explain the ideas rather than detailed implementation explanation. I'm sorry for my bad English, so please tell me if something is not clear in the descriptions.
Two Bags of Potatoes
The author of this problem is Gerald. The total number of potatoes is a multiple of k and constraint 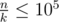 there will be at most 105 multiples of k in range 1 to n. So you can iterate on multiples of k and print the ones that satisfy the problem.
there will be at most 105 multiples of k in range 1 to n. So you can iterate on multiples of k and print the ones that satisfy the problem.
Easy Tape Programming
In this problem you just need to simulate every thing which is written in the statement step by step. You can see a simple implementation of this here: http://www.codeforces.com/contest/239/submission/2512422
Not Wool Sequences
Let a1, ..., an be a not-wool-sequence. We define another sequence called b in which bi is xor of the first i elements of a, 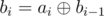 and b0 = 0.
and b0 = 0.
Now xor of elements of a consecutive subsequence like ai, ..., aj will be equal to 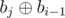 . So we know that all elements of b should be different. Therefore b is a sequence of distinct integers of length n + 1 starting with 0 made of numbers 0 to 2m - 1. The number of such sequences is
. So we know that all elements of b should be different. Therefore b is a sequence of distinct integers of length n + 1 starting with 0 made of numbers 0 to 2m - 1. The number of such sequences is 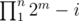 and this is the answer to problem.
and this is the answer to problem.
Boring Partition
Coming soon...
World Eater Brothers
Consider we only want to change direction of minimum number of roads so that all other countries are reachable from a specific country x. This problem can be solved in O(n) and it's exactly what 219D - Choosing Capital for Treeland asks for. If you don't know how to solve it you can read the editorial of that contest.
Consider two countries A and B which can be chosen by world eater brothers to achieve the minimum number of road direction changes. After changing the direction of roads, there exists a country on the undirected path between A and B which is reachable from both A and B using roads. We call such country a middle-country.
We want to iterate on middle-countries and find the best two countries for ruling for each middle-country. For each neighbor of the current middle-country calculate the minimum number of road changes in the subtree rooted at that neighbor so that all countries will be reachable from some country in that subtree. Then from two of these subtrees we need to pick A and B and all other subtrees will have edges pointing to the root of subtree. This can be computed in O(n) for each middle-city. So the overall complexity will be O(n2).
Tape Programming
This problem was my favorite in the problemset. The primary point is that at any moment during the interpretation of a program only a prefix of the program is modified and used by IP.
Consider we want to calculate the output of subsequence sl, ..., sr. While running the original program s1, ..., sn if at any moment CP enters the interval [l, r] it should be pointing to position l and the direction of DP should be right. So it's like we have started interpreting sl, ..., sr independently. The termination of execution of sl, ..., sr is the first time CP points to somewhere outside interval [l, r].
Therefore what we need to solve the problem is to run the original program. And after each termination if the program is nonempty then run it again until program is empty. Then we should keep a log of positions we have visited and the time of each visit and the number of printed digits of each type until then. After this preprocessing the to calculate the answer of query (li, ri) its enough to find the first time CP visited sli and the first time CP visited sri + 1 or sli - 1 after that.
The described approach can be implemented in O(nlog(n) + qlog(n)).
Meeting her
Consider a bus passing a shortest path from si to ti. There are some points that are necessary to pass in order to obtain a shortest path. Firstly we compute them. This can be done in O(n3) with Floyd-Warshall and some processing after that. Urpal is sure that a bus from i-th company always passes such vertices on his path from si to ti. So he can get on a bus from i-th company only at vertices the bus surely passes.
At any moment Urpal's status can be uniquely determined by his position on the map and the bus he's traveling with. So we have nk states (position, bus).
Our goal is to reach some (b, ...) state from a (a, v) state which bus v surely passes a (source states). So let's find all states that can reach a goal state. We call such states good states.
Consider Urpal is at junction x and he's traveling with a bus of type y. Let v1, v2, ..., vw be the list of junctions the bus might go on its shortest path from sy to ty. And let c1, c2, ..., cl be the list of companies that their bus surely passes junction x, excluding y-th company. For state (x, y) we know we can reach junction b (it's a good state) if one of the following is true:
- x = b, the minimum cost of solving the problem will be 0.
- All states (v1, y), (v2, y), ... and (vw, y) are good states, the minimum cost of solving the problem will be the maximum of all these states.
- At least one of states (x, c1), (x, c2), ... or (x, cl) is a good state, the minimum cost of solving the problem will be the minimum the good ones plus one.
At first the only good states we know are states with junction b, (b, ...). Now some new states might have become good states. So we add those states to the list of known good states. We do this until no state becomes good anymore.
At the end we print the minimum cost of source states which are good, and if they don't exist we print -1.
The process thing can be implemented in O(n4). :)











World Eater Brothers can be solved in O(n) using dp on tree. Generally let the number of choosing vertices be m (in original problem m = 2), then it can be solved in O(n * m). On each sub-tree we keep the number of points already chosen (or to be chosen) and flag indicating if root vertex of this sub-tree is covered (reachable from any vertex we chose). On each step we choose the direction of one edge
Can you please detail a bit your solution? I do not understand what is the meaning of the dp and how you build it. Thank you!
Let's call the vertex to be covered if it is reachable from any vertex we've already chosen. We should cover all the vertices.
The state of dp is a sub-tree (i. e. an edge, each edge uniquely defines not empty for edges sub-tree), how many points to be chosen and a flag, indicating if a root of sub-tree is covered.
On each step we choose the direction of current edge. Our goal is to find minimum of several sums. Each sum is composed of states of 2 sub-trees (child down sub-tree and current right sub-tree) + the cost of this direction.
There is also another necessary move — to choose the current vertex — root of sub-tree (if it is not covered). It is a direct move from one state of dp to another
Moves:
The root is not covered
Edge down
Current vertex is still not covered but it will be covered
Down sub-tree: covered
Right sub-tee: not covered
Edge up
Down sub-tree covers current vertex
Down sub-tree: not covered
Right sub-tree: covered
The root is covered
Edge down
Down sub-tree: covered
Right sub-tee: covered
Edge up
Down sub-tree: not covered
Right sub-tee: covered
Tape Programming can be implemented in O(d * (N + Q)), where d is number of different digits (which is 10, of course, but IMO should be mentioned for clarity).
We emulate given program workflow and for each position store a queue of events "entering segment from query i" or "leaving segment from query i". Also we store how many times we printed every digit. When moving to new position we process all events for it. For "entering" event mark the query as "active", memorize current digit counts for this query and generate two new "leaving" events in positions li - 1 and ri + 1. For "leaving" event, if the query is "active", store current digit counts MINUS previously remembered counts as answer for the query and mark it as "non-active". Also, process current command and change things if needed. If there are no "active" queries at the moment, we can terminate to no harm. If some query wasn't answered, start anew from first non-visited symbol.
Though my solution sent during the contest used Fenwick tree for finding the answer. =)
You English is excellent and excellent tutorial. I have a doubt in Problem C Div 2.What is the reason for calculating length n+1, shouldn't it be n as specified in the question.And when you are applying the formula your i varies from 1 to n whereas, when I solved i varies from 0 to n-1. I solved (2^m)Pn to get to the formula,where P is the permutation.Please guide where am I wrong.
The new array b you create should be indexed from 0 to n cause when you want to calculate you need to calculate
you need to calculate 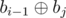 . So when i = 1 we need b0 to exist and it should be equal to 0.
. So when i = 1 we need b0 to exist and it should be equal to 0.
waiting for Boring Partition tutorial , its boring process :D
Let me give a hint :) Calculate answer for two sets and choose the best one (for n > 2):
Others distributions are not effective.
Can you prove it?
We have the biggest pair: a[n] + a[n-1]; We have the smallest pair: a[0] + a[1]; So, the answer for a[0]..a[n] in one set is:
We can try to make it better, but there is a sense to move only one value (among a[n], a[n-1], a[1], a[0]) to another set. Because if two or more of them are moved, we can get +h or +0 to answer, not better. So, try to put a[0] in second set and check, if the answer becomes better. There are also no sense trying to move a[k] (k > 0) to another set, because the extreme possible minimum (a[0] + a[1] + h) has been alredy reached, but there is a danger to increase the maximum.
Solution for B — div 1:
Sort all a[i], then check all partitions where a[0]..a[pos] are in the first group and a[pos+1]..a[n-1] — in the second group. Choose best of them.
My solution with the only check for pos = 0 was also accepted
Boring partition:
Sort the array in non-increasing order. Array size is n, numbering starts from 1. If we kept all the integers in the same subsequence, the answer would be (a[1] + a[2]) — (a[n-1] + a[n]), which is the difference between the maximal and minimal possible sums, respectively. To make the difference smaller, we need to either : decrease the maximal sum or increase the minimal sum. Since h >= 0, moving a number to another subsequence can only increase the sums. Hence it's impossible to decrease the current maximal sum, so we should try to increase the minimal sum. To do that, we should move the smallest element, a[n], to the other subsequence. Now, a few different scenarios can happen:
1) Maximal sum remains a[1] + a[2], minimal sum becomes a[n-1] + a[n] + h, the difference becomes smaller (or equal, if h = 0).
2) Maximal sum remains a[1] + a[2], minimal sum becomes a[n-2] + a[n-1], the difference becomes smaller (or equal, if a[n-2] = a[n]).
3) Maximal sum becomes a[1] + a[n] + h, minimal sum becomes a[n-2] + a[n-1]. The difference can be larger, equal or smaller.
Moving more numbers to the other subsequence can't decrease the difference in any scenario. In conclusion, the answer is always either:
1) Keep everything in the same subsequence.
2) Keep everything in the same subsequence, except the smallest element.
thanks :)
Could you please detail a bit your explatation for World Eater Brothers? I could not fully get it. What's the meaning of 'upward' and 'min' in your source?
Consider vertex v as the middle-country of the optimal answer. If this vertex has k neighbors, each neighbor has it's own subtree. We know that the two capitals will be in different subtrees, because this vertex is middle-country. The other k - 2 subtrees should be directed subtrees with all vertices able to reach v. So for each subtree we compute the minimum number of changes in directions in order to have a capital there and the number of changes so that all vertices point to v. Then we pick two subtrees for capitals and the others should have edges pointing to v.
Sorry for the delay in answering. Last day I had unknown problems about posting comments!
Excuse me, can you give me a simple demonstration on Div1 — A? I still can't understand it.
We should know that for any array b as we defined in the solution we can make array a.
A sequence a is a wool sequence if there are two equal elements in its corresponding sequence b, like bi and bj so that i < j. Because shows
shows  . So in this case we have xor of a continuous subsequence equal to zero.
. So in this case we have xor of a continuous subsequence equal to zero.
For example if a is (1, 3, 1) then b would be (0, 1, 2, 3).
""The number of such sequences is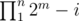 and this is the answer to problem."" Can you please give me a proof?
and this is the answer to problem."" Can you please give me a proof?
The sequence b should include different numbers. We have numbers from 1 to 2^m. Zero we can't choose as it will be wool sequence a. As first number of sequence b we can choose 2^m-1 numbers, as second 2^m-2 ( as we have chosen one number before and we can't repeat it again), for third 2^m-3 and so on. This is all.
You have a typo there. It should be.. A sequence a is a wool sequence if there are "NO" two equal elements in its corresponding sequence b, like bi and bj so that i < j.