Let's discuss the problems!!!
How to solve E, J?
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3640 |
| 2 | Benq | 3593 |
| 3 | tourist | 3572 |
| 4 | orzdevinwang | 3561 |
| 5 | cnnfls_csy | 3539 |
| 6 | ecnerwala | 3534 |
| 7 | Radewoosh | 3532 |
| 8 | gyh20 | 3447 |
| 9 | Rebelz | 3409 |
| 10 | Geothermal | 3408 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 163 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Let's discuss the problems!!!
How to solve E, J?
| Name |
|---|



how to solve C and F?
C: Possible leaders are those who have at least (n — 1)/2 edges. Now if leader is fixed, it's optimal to put every his friend to separate team and to put others we may find matching in O(NM). There are at most O(m / n) leaders so overall complexity is O(m^2)
My explanation is probably hard to understand but anyway:
F: notice that letter at position i goes to either i/2 or (i — 1)/2 + n / 2. Now if you will see it in reverse it is from i to 2i mod (n — 1).
Now we have letters on the cycle in
sand letters intin same positions. We need to get possible cyclical shifts that will move string generated fromsto string generated fromt. Using prefix function (or probably z function works too) we get possible shifts (they give some reminders module len of the cycle which is divisor of phi(n — 1)Code
I found that we have to make multiplicative order of 2 modulo n+1 (n is the size of string) shuffles to get original string again. Can one continue from this?
You can calculate hashs and easily check
Why the length of the cycle is divisor of phi(n)? I just noticed that lcm of length is <= n. So I just took a marker array of length lcm.
It's actually is divisor of
phi(n - 1)(fixed typo) and it comes from the fact, that we examine numbers 2^k mod (n — 1). And it's actually divisor of order of 2 modulo (n — 1) which is divisor of number of elements which are coprime to n — 1How to solve I?
Choose x such that no matter what happens, the value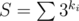 decreases to at most (2 / 3)S.
decreases to at most (2 / 3)S.
Are there any other problems that use similar techniques?
Controlling the sum of powers of a fixed base reminds me of a certain IMO problem, but there it served the other player in the interactive game.
And I thought nobody would be crazy enough to use powers of 3 (powers of 4 work the best among whole numbers).
Why it works?
You divide into two groups(overlapping by 1 number) so that at least one half will be removed. This half is divided by 3. So you decrease result at least by S/2*2/3=S/3
E: Let {x} = x - [x] be the fractional part of x. We want to compute [N / 11] + [N / 111] + ... = N * (1 / 11 + 1 / 111 + ...) - {N / 11} - {N / 111} - .
To compute N * (1 / 11 + 1 / 111 + ...) approximately, find the decimal representation of (1 / 11 + 1 / 111 + ...), and use FFT.
To compute {N / 11} = {9N / 100 + 9N / 10000 + 9N / 1000000...}, we only need the values of {9N / 10k}, so we pre-compute these values in double. You should be very careful to avoid precision issues.
What did you do to avoid precision issues? I used a lot of computer time to generate tests where one division result is very close to a whole number... (I am the author)
It seems I just added epsilon before rounding and used long doubles (I hoped that the input can't be very tricky because they are randomly generated). So, is the intended solution different?
You are supposed to fallback to precise division if result is too close to a whole number. Random generation guarantees that there are only O(1) fallbacks (no more than 1 in practice).
So the intended solution also involves floating-point calculation?
I tried the same idea with rng_58. But, keep receiving WA on test 40. The precision issue when calculating the fractional part is very significant. Is there any good way to deal with it?
I used 64-bit integer numbers for fixed point decimal arithmetic. So I can calculate exactly how precise my result is. If it falls on an edge, I use fallback with exact division.
J: sqrt decomposition. How to solve B??
B looks quite easy idea-wise. Let (u, v) be an edge, and let T(u, v) be a tree rooted at v we get when we remove the edge. Note that T(u, v) and T(v, u) are different.
Then, find the probabilistic distribution of the depth of T(u, v). This can be done by some integrations, and it will be piecewise polynomial.
To compute the answer, for each edge (u, v), find the expected depths of T(u, v), T(v, u), and the expected length of the edge (u, v), given that the midpoint of the diameter lies on this edge. Again this can be done by some integrations.
Note that we need "all-direction DP" to achieve O(N4).
I think you underestimate the brilliance of your idea: if l(t) is the depth of the subtree rooted at t, and e is the length of the edge connecting u and v, then the condition that the midpoint of the diameter lies on edge (u, v) is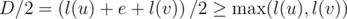 , and this condition immediately implies you don't need to look at the diameters of the subtrees at all, since the diameter of the subtree is never greater than 2l(t), which is less than D anyway if the condition is true. I find this observation quite beautiful and I didn't notice it myself during the contest, even though it seems kinda obvious after you notice.
, and this condition immediately implies you don't need to look at the diameters of the subtrees at all, since the diameter of the subtree is never greater than 2l(t), which is less than D anyway if the condition is true. I find this observation quite beautiful and I didn't notice it myself during the contest, even though it seems kinda obvious after you notice.
The other part of the solution doesn't seem so beautiful: we can compute the CDF of the depth distribution of a given vertex by multiplying the CDFs for all children (since max(a, b) ≤ t is equivalent to a ≤ t and b ≤ t and they are independent), and by applying the transformation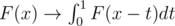 (it's exactly what happens if we add an edge with a uniformly distributed length). Then it's clear that F is always a polynomial on every segment [a, a + 1] for integer values of a of degree at most n.
(it's exactly what happens if we add an edge with a uniformly distributed length). Then it's clear that F is always a polynomial on every segment [a, a + 1] for integer values of a of degree at most n.
Or is there an easier approach?
I'm glad you liked the idea of tracking the diameter structure by restricting the tree center location. This is exactly an intended solution.
Could please explain how to apply sqrt? To requests and store best pairs(max staircase 1, max staircase 2)?
Intended solution for J is O(n log n) btw, though with a huge constant. I'll describe it in comments later.
So what's the idea of the intended solution? Any hint?
dp[i][j] = optimal cost for [i, N] if the second maximum has the value >= j (and the first maximum is implicitly pre[i] = maximum value for prefix i)
dp[i][v[i]] = dp[i + 1][v[i]]
dp[i][j < v[i]] = min{dp[i + 1][j] + pre[i] — v[i], dp[i][v[i]]}
dp[i][j > v[i]] = dp[i + 1][j] + j — v[i]
First observation: Something is fishy about how to calculate dp[i][j > v[i]], the reccurence uses "j" as the second maximum while the definition of the dp says the maximum can be higher, so should be adding more than j. But we don't need to do that, because in our computations dp[i][j] will influence only some dp[i' < i][k <= j], so it is actually worse — but it's pessimistic dp and it really works.
Second observation: dp[i][j] is now increasing as j increases. So we can use a segment tree with some lazy propagations to keep the dp states as we decrease i.
How to solve G?
Notice that WLOG we can assume that the ai are the inner n - 1 points of the broken line graph, because there should a change of slope in a point ai if it's λi is nonzero.
Also, we can easily calculate the needed λi-s from the changes of slope of the broken line. Now, just check if the graph of the sum using those λi-s and ai-s is indeed the broken line from the input. You can check only two points from each linear segment and ray, because two linear functions are equal when they agree on two points. Equality checking can be done exactly or with high probability using fraction arithmetic or some other methods.
What interests me the most about this problem is the weird nature of the precision issues we have been experiencing when using floating point operations. Why exactly is it bad to choose the ai-s for checking the equality of the functions? What is the maximum error in calculations and how to make sure it isn't reached?
It is an intended way of thinking about this problem, but if you choose not to implement it also fighting against precision issues, but to think a bit more what the obtained formulas mean, you may prove the following criteria:
The answer is Yes if and only if leftmost and rightmost rays of the plot 1) have slopes that are opposite to each other (i.e. have the same absolute value but the opposite sign) and 2) when extended to lines, have intersection point on OX axis or are parallel to OX and OX is located exactly at the middle between them.
These checks may be performed easily in an integral data type.
But when thinking on this problem for the first time by myself, I stopped on exactly the same moment as you and performed all the calculations modulo large random prime.
I calculated the values, but for some reason keep on getting WA on test #86. What precision values did you use to check for equality?
We got OK with __float128 and eps = 10 - 12
What about D?
The intended solution utilizes the following fact. Consider the sequence of contiguous groups of people from the same team. Then it is true that this sequence is modified only via extending one of the existing groups by a new person from the same team, or by creating a new single-person group at the end of the line.
Now store two data structures: a segment tree keeping sizes of all groups in order from head of the queue to its tail, and a vector of group indices for each of the teams. When a new person comes, first find the group he would get into if there was no restriction of having a neighboring teammate, and then, using a single lower bound query in the corresponding team vector, move to the closest group of people from his team.
This contest is in Gym now: 2018 Petrozavodsk Winter Camp, Yandex Cup
Yes, it is the same contest as Grand Prix of Khamovniki.
(Khamovniki is a district in Moscow where the main Yandex office is situated)
How to solve A?